
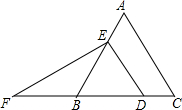
 如圖,在等邊△ABC中,點D、E分別在邊BC、AB上,且DE∥AC,過點E作EF⊥DE,交CB的延長線于點F.若BD=5,則EF2=75.
如圖,在等邊△ABC中,點D、E分別在邊BC、AB上,且DE∥AC,過點E作EF⊥DE,交CB的延長線于點F.若BD=5,則EF2=75. 分析 根據平行線的性質可得∠EDB=∠C=60°,進而可證明△EDB是等邊三角形,再根據勾股定理即可求解EF的長.
解答 解:∵△ABC是等邊三角形,
∴∠C=60°,
∵DE∥AC,
∴∠EDB=∠C=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDB=30°,
∵∠ABC=60°,∠EDB=60°,
∴△EDB是等邊三角形.
∴ED=BD=5,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=10,
∴EF2=DF2-DE2=75.
故答案為:75.
點評 本題考查了等邊三角形的判定與性質,以及勾股定理的運用和30度的銳角所對的直角邊等于斜邊的一半的性質,求出DF的長是解題關鍵.


科目:初中數學 來源:2017屆湖北省襄陽市九年級下學期第一次月考數學試卷(解析版) 題型:單選題
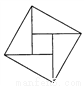
2002年8月在北京召開的國際數學家大會會徽取材于我國古代數學家趙爽的《勾股圓方圖》,它是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形,如圖所示,如果大正方形的面積是13,小正方形的面積是1,直角三角形的短直角邊為 ,較長直角邊為
,較長直角邊為 ,那么
,那么 的值為( )
的值為( )
A. 13 B. 19 C. 25 D. 169
查看答案和解析>>
科目:初中數學 來源:2016-2017學年湖北省武漢市侏儒山街四校八年級3月月考數學試卷(解析版) 題型:單選題
下列二次根式中,屬于最簡二次根式的是( )
A. 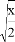 B.
B. 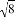 C.
C. 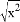 D.
D.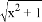
查看答案和解析>>
科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:單選題
下列四組條件中,不能判定四邊形ABCD是平行四邊形的是( )
A. AB=DC,AD=BC B. AB∥DC,AD∥BC,
C. AB∥DC,AD=BC D. AB∥DC,AB=DC
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a=2,b=3 | B. | a=2,b=-3 | C. | a=-2,b=3 | D. | a=-2,b=-3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com