Question

如圖，直線y=﹣x+3與x軸，y軸分別交于B，C兩點，拋物線y=﹣x²+bx+c經過B，C兩點，點A是拋物線與x軸的另一個交點．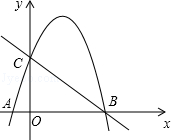

（1）求B、C兩點坐標；
（2）求此拋物線的函數解析式；
（3）在拋物線上是否存在點P，使S_△PAB=S_△CAB，若存在，求出P點坐標，若不存在，請說明理由．

Answer 1

（1）B（3，0）C（0，3）（2）此拋物線的解析式為y=﹣x²+2x+3．（3）存在這樣的P點，其坐標為P（0，3），（2，3）（1+，﹣3）或（1﹣，﹣3）．

解析試題分析：（1）已知了過B、C兩點的直線的解析式，當x=0時可求出C點的坐標，當y=0是可求出B點的坐標．
（2）由于拋物線的解析式中只有兩個待定系數，因此將B、C兩點的坐標代入拋物線中即可求出拋物線的解析式．
（3）根據（2）的拋物線的解析式可得出A點的坐標，由此可求出AB的長，由于S_△PAB=S_△CAB，而AB邊為定值．由此可求出P點的縱坐標，然后將P點的縱坐標代入拋物線的解析式中即可求出P點的坐標．
試題解析：（1）∵直線y=﹣x+3經過B、C
∴當x=0時y=3
當y=0時x=3
∴B（3，0）C（0，3）
（2）∵拋物線y=﹣x²+bx+c經過B、C
∴．
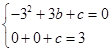∴b=2，c=3．
∴此拋物線的解析式為y=﹣x²+2x+3．
（3）當y=0時，﹣x²+2x+3=0；x₁=﹣1，x₂=3．
∴A（﹣1，0）
設P（x，y）
∵S_△PAB=S_△CAB
∴×4×|y|=×4×3
∴y=3或y=﹣3
①當y=3時，3=﹣x²+2x+3
∴x₁=0，x₂=2
P（0，3）或（2，3）
②當y=﹣3時，﹣3=﹣x²+2x+3
∴x₁=1+，x₂=1﹣
∴P（1+，﹣3）或（1﹣，﹣3）．
因此存在這樣的P點，其坐標為P（0，3），（2，3）（1+，﹣3）或（1﹣，﹣3）．
考點：二次函數綜合題．