
| 產銷商品件數(x/件) | 10 | 20 | 30 |
| 產銷成本(C/元) | 120 | 180 | 260 |
分析 (1)根據題意設出C與x的函數關系式,然后根據表格中的數據即可解答本題;
(2)根據題意可以列出相應的方程,從而可以解答本題;
(3)根據題意可以得到利潤與銷售價格的關系式,然后化為頂點式即可解答本題.
解答 解:(1)設C=ax2+bx+c,
$\left\{\begin{array}{l}{a×1{0}^{2}+10b+c=120}\\{a×2{0}^{2}+20b+c=180}\\{a×3{0}^{2}+30b+c=260}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=\frac{1}{10}}\\{b=3}\\{c=80}\end{array}\right.$,
即產銷成本C與商品件數x的函數關系式是:C=$\frac{1}{10}$x2+3x+80;
(2)依題意,得
(35-$\frac{1}{10}$x)•x-($\frac{1}{10}$x2+3x+80)=220;
解得,x1=10,x2=150,
∵每個周期產銷商品件數控制在100以內,
∴x=10.
即該公司每個周期產銷10件商品時,利潤達到220元;
(3)設每個周期的產銷利潤為y元,
∵y=(35-$\frac{1}{10}$x)•x-($\frac{1}{10}$x2+3x+80)=-$\frac{1}{5}$x2+32x-80=-$\frac{1}{5}$(x-80)2+1200,
∴當x=80時,函數有最大值,此時y=1200,
即當每個周期產銷80件商品時,產銷利潤最大,最大值為1200 元.
點評 本題考查二次函數的應用、一元二次方程的應用,解題的關鍵是明確題意,找出所求問題需要的條件.


科目:初中數學 來源: 題型:解答題
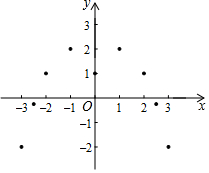 某“數學興趣小組”根據學習函數的經驗,對函數y=-x2+2|x|+1的圖象和性質進行了探究,探究過程如下,請補充完整:
某“數學興趣小組”根據學習函數的經驗,對函數y=-x2+2|x|+1的圖象和性質進行了探究,探究過程如下,請補充完整:| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | m | 2 | 1 | 2 | 1 | -$\frac{1}{4}$ | -2 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
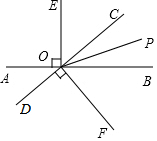 如圖,直線AB與CD相交于點O,OP是∠BOC的平分線,OE⊥AB,OF⊥CD.
如圖,直線AB與CD相交于點O,OP是∠BOC的平分線,OE⊥AB,OF⊥CD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.506×108 | B. | 1.506×107 | C. | 15.06×106 | D. | 15.06×107 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com