⊙O的半徑為1,以O為原點建立直角坐標系,正方形ABCD的頂點B的坐標為(5,0),點D在⊙O上運動,當CD與圓相切時,直線OD的解析式為 .
【答案】
分析:分兩種情況:①D
1點在第二象限時;②D
2點在第四象限時;再根據相似三角形的性質,可得比例關系式,代入數據可得CD所在直線對應的函數關系.
解答: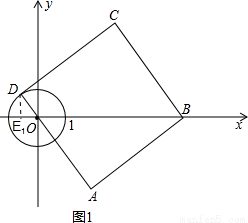
解:直線CD與⊙O相切分兩種情況:
①如圖1,設D
1點在第二象限時,
過D
1作D
1E
1⊥x軸于點E
1,設此時的正方形的邊長為a,
∴(a-1)
2+a
2=5
2,
∴a=4或a=-3(舍去),
∵Rt△BOA∽Rt△D
1OE
1
∴
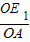
=
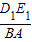
=
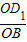
,
∴OE
1=

,D
1E
1=

,
∴D
1(-

,

),
代入y=kx,

=-

k,
∴k=-

,
∴直線OD的函數關系式為y=-

x,
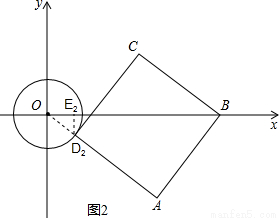
②如圖2,設D
2點在第四象限時,過D
2作D
2E
2⊥x軸于點E
2,
設此時的正方形的邊長為b,則(b+1)
2+b
2=5
2,
解得b=3或b=-4(舍去).
∵Rt△BOA∽Rt△D
2OE
2,
∴
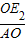
=
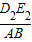
=
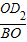
,
∴OE
2=

,D
2E
2=

,
∴D
2(

,-

),
代入y=ax,
-

=

a,
∴k=-

,
∴直線OD的函數關系式為y=-

x,
故答案為:y=-
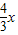
或y=-

x.
點評:此題主要考查了一次函數的綜合應用,本題難度較大,要求學生有較強的綜合分析能力及數形結合分析解決問題的能力.

 解:直線CD與⊙O相切分兩種情況:
解:直線CD與⊙O相切分兩種情況: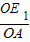 =
=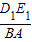 =
=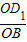 ,
, ,D1E1=
,D1E1= ,
, ,
, ),
), =-
=- k,
k, ,
, x,
x,
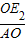 =
=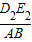 =
=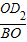 ,
, ,D2E2=
,D2E2= ,
, ,-
,- ),
), =
= a,
a, ,
, x,
x,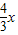 或y=-
或y=- x.
x.

 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案 已知⊙O的半徑為1,以O為原點,建立如圖所示的直角坐標系.有一個正方形ABCD,頂點B的坐標為(-
已知⊙O的半徑為1,以O為原點,建立如圖所示的直角坐標系.有一個正方形ABCD,頂點B的坐標為(-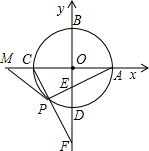 如圖,以⊙O兩條互相垂直的直徑所在直線為軸建立平面直角坐標系,兩坐標軸交⊙O于A,B,C,D四點,點P在弧CD上,連PA交y軸于點E,連CP并延長交y軸于點F.
如圖,以⊙O兩條互相垂直的直徑所在直線為軸建立平面直角坐標系,兩坐標軸交⊙O于A,B,C,D四點,點P在弧CD上,連PA交y軸于點E,連CP并延長交y軸于點F.