
 如圖,已知直線y=
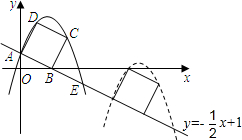
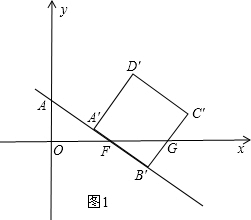
如圖,已知直線y=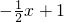 交坐標軸于A,B 兩點,以線段AB為邊向上作正方形ABCD,過點A,D,C的拋物線與直線另一個交點為E.
交坐標軸于A,B 兩點,以線段AB為邊向上作正方形ABCD,過點A,D,C的拋物線與直線另一個交點為E. 個單位長度的速度沿射線AB下滑,直至頂點D落在x軸上時停止.設正方形落在x軸下方部分的面積為S,求S關于滑行時間t的函數關系式,并寫出相應自變量t的取值范圍.
個單位長度的速度沿射線AB下滑,直至頂點D落在x軸上時停止.設正方形落在x軸下方部分的面積為S,求S關于滑行時間t的函數關系式,并寫出相應自變量t的取值范圍.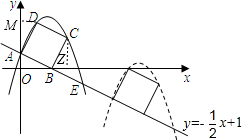 ∵直線y=
∵直線y=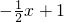 ,
,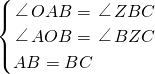 ,
,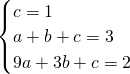 ,
, 解得:a=-
解得:a=- ,b=
,b=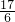 ,c=1,
,c=1, x2+
x2+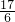 x+1;
x+1; ,
,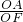 =
= ,
,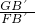 =
=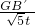 =
= ,
, t,
t,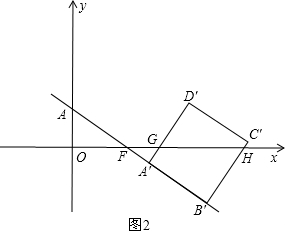 ∴S△FB′G=
∴S△FB′G= FB′×GB′=
FB′×GB′= •
• t•
t• t,
t, t2;
t2; ,
, t-
t- ,
,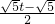 ,
, t,
t, (A′G+B′H)•A′B′=
(A′G+B′H)•A′B′= •(
•(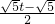 +
+ t)
t)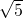 ,
, t-
t- ;
;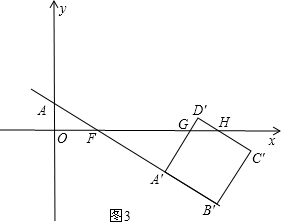 當2<t≤3時,如圖3,
當2<t≤3時,如圖3,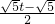 ,
, -
-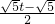 =
=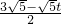 ,
, ×2×1=1,OA=1,∠AOF=∠FA′G=90°,∠AFO=∠GFA′,
×2×1=1,OA=1,∠AOF=∠FA′G=90°,∠AFO=∠GFA′,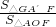 =(
=(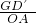 )2,
)2,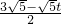 )2,
)2, )2-(
)2-(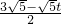 )2,
)2, t2+
t2+ t-
t- .
.

 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:初中數學 來源: 題型:
| 1 |
| 2x |
 第一象內的點過點P作PM⊥x軸于M、PN⊥y軸于N.兩垂線與直線AB交于E、F.
第一象內的點過點P作PM⊥x軸于M、PN⊥y軸于N.兩垂線與直線AB交于E、F.| 1 |
| 2x |
查看答案和解析>>
科目:初中數學 來源: 題型:
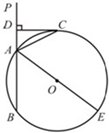 23、如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,點C為⊙O上一點,且AC平分∠PAE,過C作CD丄PA,垂足為D.
23、如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,點C為⊙O上一點,且AC平分∠PAE,過C作CD丄PA,垂足為D.查看答案和解析>>
科目:初中數學 來源: 題型:
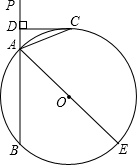 (2012•昌平區一模)如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,C為⊙O上一點,且AC平分∠PAE,過點C作CD⊥PA于D.
(2012•昌平區一模)如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,C為⊙O上一點,且AC平分∠PAE,過點C作CD⊥PA于D.查看答案和解析>>
科目:初中數學 來源: 題型:
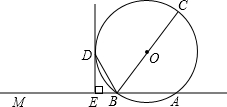 如圖,已知直線MA交⊙O于A、B兩點,BC是⊙O的直徑,點D在⊙O上,且BD平分∠MBC,過D作DE⊥MA,垂足為E.
如圖,已知直線MA交⊙O于A、B兩點,BC是⊙O的直徑,點D在⊙O上,且BD平分∠MBC,過D作DE⊥MA,垂足為E.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,點C為⊙O上一點,且AC平分∠PAE,過C作CD⊥PA,垂足為D.
如圖,已知直線PA交⊙O于A、B兩點,AE是⊙O的直徑,點C為⊙O上一點,且AC平分∠PAE,過C作CD⊥PA,垂足為D.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com