Question

7．O為直線DA上一點(diǎn)，OB⊥OF，EO是∠AOB的平分線．

（1）如圖（1），若∠AOB=130°，求∠EOF的度數(shù)；
（2）若∠AOB=α，90°＜α＜180°，求∠EOF的度數(shù)；
（3）若∠AOB=α，0°＜α＜90°，請(qǐng)?jiān)趫D（2）中畫出射線OF，使得（2）中∠EOF的結(jié)果仍然成立．

Answer 1

分析 （1）首先利用角平分線的定義可得∠AOE的度數(shù)，由垂直的定義得∠BOF=90°，易得∠AOF，可得∠EOF；
（2）首先利用角平分線的定義可得∠AOE=$\frac{1}{2}α$，由垂直的定義得∠BOF=90°，易得∠AOF=α-90°，可得∠EOF；
（3）根據(jù)題意OB⊥OF，使得（2）中∠EOF的結(jié)果仍然成立，畫出射線OF即可，再結(jié)合圖形同理（2）可得結(jié)果．

解答 解：（1）∵∠AOB=130°，EO是∠AOB的平分線，
∴$∠AOE=\frac{1}{2}∠AOB=\frac{1}{2}×130°$=65°，
∵OB⊥OF，
∴∠BOF=90°，
∴∠AOF=∠AOB-∠BOF=130°-90°=40°，
∴∠EOF=∠AOE-∠AOF=65°-40°=25°；

（2）∵∠AOB=α，90°＜α＜180°，EO是∠AOB的平分線，
∴∠AOE=$\frac{1}{2}α$，
∵∠BOF=90°，
∴∠AOF=α-90°，
∴∠EOF=∠AOE-∠AOF=$\frac{1}{2}α$-（α-90°）=90$°-\frac{1}{2}α$；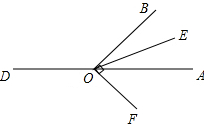

（3）如圖，∵∠AOB=α，0°＜α＜90°，
∴∠BOE=∠AOE=$\frac{1}{2}α$，
∵∠BOF=90°，
∴∠EOF=∠BOF-∠BOE=90$°-\frac{1}{2}α$．

點(diǎn)評(píng) 本題主要考查了角平分線的定義和垂直的定義，結(jié)合圖形利用角平分線的定義和垂直的定義是解答此題的關(guān)鍵．