
 如圖,直角坐標(biāo)系中,點A的坐標(biāo)為(1,0),以線段OA為邊在第四象限內(nèi)作等邊△AOB,點C為x正半軸上一動點(OC>1),連接BC,以線段BC為邊在第四象限內(nèi)作等邊△CBD,直線DA交y軸于點E.
如圖,直角坐標(biāo)系中,點A的坐標(biāo)為(1,0),以線段OA為邊在第四象限內(nèi)作等邊△AOB,點C為x正半軸上一動點(OC>1),連接BC,以線段BC為邊在第四象限內(nèi)作等邊△CBD,直線DA交y軸于點E.分析 (1)判斷△OBC與△ABD全等,由等邊△AOB和等邊△CBD得到全等條件;
(2)設(shè)P(0,m),延長AB交y軸于F,在Rt△OAF中,由OA=1,∠AFO=30°,推出OF=$\sqrt{3}$OA=$\sqrt{3}$,根據(jù)S△PAB=S△PAF-S△PBF,可得2=$\frac{1}{2}$(m+$\sqrt{3}$)•1-$\frac{1}{2}$(m+$\sqrt{3}$)•$\frac{1}{2}$,解方程求出m,即可解決問題.
(3)根據(jù)(1)容易得到∠OAE=60°,然后在中根據(jù)直角三角形30°,所對的直角邊等于斜邊的一半可以得到AE=2,從而得到E的坐標(biāo)是固定的.
解答 解:(1)△OBC≌△ABD,
理由:∵△AOB是等邊三角形,
∴OB=AB,∠OBA=∠OAB=60°,
又∵△CBD是等邊三角形
∴BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
$\left\{\begin{array}{l}{OB=AB}\\{∠OBC=∠ABD}\\{BC=BD}\end{array}\right.$,
∴△OBC≌△ABD(SAS).
(2)設(shè)P(0,m),延長AB交y軸于F,
在Rt△OAF中,∵OA=1,∠AFO=30°,
∴OF=$\sqrt{3}$OA=$\sqrt{3}$,
∵S△PAB=S△PAF-S△PBF,
∴2=$\frac{1}{2}$(m+$\sqrt{3}$)•1-$\frac{1}{2}$(m+$\sqrt{3}$)•$\frac{1}{2}$,
∴m=8-$\sqrt{3}$,
∴點P坐標(biāo)為(0,8-$\sqrt{3}$),
根據(jù)對稱性,P關(guān)于點F的對稱點P′也滿足條件,P′(0,-8-$\sqrt{3}$),
綜上所述,滿足條件的點P坐標(biāo)為(0,8-$\sqrt{3}$)或(0,-8-$\sqrt{3}$).
(3)∵△OBC≌△ABD,
∵∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,
∵∠OAE=60°,
∴∠AEO=30°,
∴AE=2OA=2,
∴OE=$\sqrt{{2}^{2}-{1}^{1}}$=$\sqrt{3}$,
∴點E的位置不會發(fā)生變化,E的坐標(biāo)為E(0,$\sqrt{3}$).
點評 本題考查三角形綜合題、全等三角形的判定和性質(zhì)、三角形的面積、勾股定理等知識,解題的關(guān)鍵是正確尋找全等三角形,學(xué)會利用分割法求三角形面積,學(xué)會用方程的思想思考問題,屬于中考壓軸題.


 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
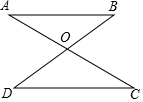 如圖,已知AB∥CD,欲證明△AOB≌△COD,可補充條件AB=CD或OA=OC或OB=OD.(填寫一個適合的條件即可)
如圖,已知AB∥CD,欲證明△AOB≌△COD,可補充條件AB=CD或OA=OC或OB=OD.(填寫一個適合的條件即可)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
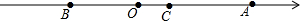 如圖,在數(shù)軸上原點O表示的數(shù)是0,B點表示的數(shù)是m,A表示的數(shù)是n,且(m+4)2+|n-8|=0.
如圖,在數(shù)軸上原點O表示的數(shù)是0,B點表示的數(shù)是m,A表示的數(shù)是n,且(m+4)2+|n-8|=0.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在平面直角坐標(biāo)系中,△OA0A1,△OA1A2,△OA2A3,△OA3A4…都是等腰直角三角形,點A0(1,0),A1(1,1),A2(0,2),A3(-2,2),A4(-4,0),…,則依圖中所示規(guī)律,A2015的坐標(biāo)為(21007,21007).
如圖,在平面直角坐標(biāo)系中,△OA0A1,△OA1A2,△OA2A3,△OA3A4…都是等腰直角三角形,點A0(1,0),A1(1,1),A2(0,2),A3(-2,2),A4(-4,0),…,則依圖中所示規(guī)律,A2015的坐標(biāo)為(21007,21007).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x≠-1 | B. | x≠2 | C. | x≠±1 | D. | x≠-1且x≠2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 一個數(shù)的絕對值等于它本身,則這個數(shù)一定是正數(shù) | |
| B. | 沒有最小的有理數(shù),也沒有絕對值最小的有理數(shù) | |
| C. | 有理數(shù)的絕對值一定是正數(shù) | |
| D. | 如果|a|=-a,那么a≤0 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com