
���}Ŀ����1����D1��![]() ��������
��������![]() ߅
߅![]() �ϵ�һ�c(di��n)���B��
�ϵ�һ�c(di��n)���B��![]() ��
��![]() ����
����![]() �@�c(di��n)
�@�c(di��n)![]() ��r(sh��)����D(zhu��n)
��r(sh��)����D(zhu��n)![]() �����D(zhu��n)��ǵă�߅�քe�c�侀
�����D(zhu��n)��ǵă�߅�քe�c�侀![]() �����c(di��n)
�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ����(xi��)������
����(xi��)������![]() ��
��![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ�����f(shu��)�����ɣ�
֮�g�Ĕ�(sh��)���P(gu��n)ϵ�����f(shu��)�����ɣ�
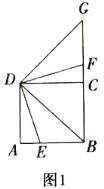
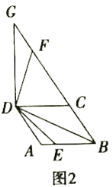
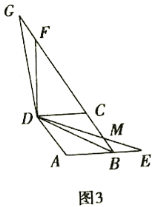
��2����(d��ng)��߅��![]() �����Σ�
������![]() ���c(di��n)
���c(di��n)![]() ������
������![]() ߅
߅![]() ����ֱ���ϵ�һ�c(di��n)���B��
����ֱ���ϵ�һ�c(di��n)���B��![]() ��
��![]() ����
����![]() �@�c(di��n)
�@�c(di��n)![]() ��r(sh��)����D(zhu��n)
��r(sh��)����D(zhu��n)![]() �����D(zhu��n)��ǵă�߅�քe�c�侀
�����D(zhu��n)��ǵă�߅�քe�c�侀![]() �����c(di��n)
�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��
��
����D2���c(di��n)![]() �ھ���
�ھ���![]() �ϕr(sh��)��Ո(q��ng)?zh��)�������
�ϕr(sh��)��Ո(q��ng)?zh��)�������![]() ��
��![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ����(xi��)���Y(ji��)Փ���o���C����
֮�g�Ĕ�(sh��)���P(gu��n)ϵ����(xi��)���Y(ji��)Փ���o���C����
����D3���c(di��n)![]() �ھ���
�ھ���![]() �����L(zh��ng)���ϕr(sh��)��
�����L(zh��ng)���ϕr(sh��)��![]() ���侀
���侀![]() ���c(di��n)
���c(di��n)![]() ����
����![]() ��
��![]() ��ֱ�ӌ�(xi��)������
��ֱ�ӌ�(xi��)������![]() ���L(zh��ng)�ȣ�
���L(zh��ng)�ȣ�
���𰸡���1��![]() ������Ҋ(ji��n)��������2����
������Ҋ(ji��n)��������2����![]() ���C��Ҋ(ji��n)��������
���C��Ҋ(ji��n)��������![]() ��
��
��������
(1)�������������|(zh��)�����D(zhu��n)�����|(zh��)�C����FDG�ա�EDB������
(2)���^(gu��)�c(di��n)![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ������(1)�е�˼·�C����FDG�ա�EDB���õ���DBG����������Σ��M(j��n)���ó���DBG=30����������ֱ��������30���Ǖr(sh��)��߅֮�Ȟ�
������(1)�е�˼·�C����FDG�ա�EDB���õ���DBG����������Σ��M(j��n)���ó���DBG=30����������ֱ��������30���Ǖr(sh��)��߅֮�Ȟ�![]() ���������
���������
���^(gu��)A�c(di��n)��AN��DB���^(gu��)D�c(di��n)��DH��GB��������DCM�ס�EBM���M(j��n)�����CM���ڡ�DCH��������DCH=60�����CH���M(j��n)���õ�![]() ���������
���������
�⣺(1) ![]() ��
��![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ�飺
֮�g�Ĕ�(sh��)���P(gu��n)ϵ�飺![]() ���������£�
���������£�
���}��֪��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ����
����![]() ��
��
��![]() ��
��
��![]() .
.

�ʴ𰸞飺![]() ��
��![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ��
֮�g�Ĕ�(sh��)���P(gu��n)ϵ��![]() .
.
��2������D2��![]() ���������£�
���������£�
�^(gu��)�c(di��n)![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �����D��ʾ��
�����D��ʾ��

������![]() ��
��![]() ��
��
�����D(zhu��n)![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ���ɵ��������εġ�������һ��֪
���ɵ��������εġ�������һ��֪
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
�O(sh��)![]() ���t
���t![]() ��
��![]() ��
��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ʴ𰸞飺![]() ��
��![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ��
֮�g�Ĕ�(sh��)���P(gu��n)ϵ��![]() .
.
���^(gu��)A�c(di��n)��AN��DB���^(gu��)D�c(di��n)��DH��GB�����D��ʾ��
��CD��BE��
���DCM�ס�EBM
��![]() �����딵(sh��)��(j��)
�����딵(sh��)��(j��)![]() �����
�����![]()
��Rt��DHC�У�����DCH=60����CD=4,��֪��HC=2
����DBA=30����AB=4��֪��BN=![]() ����BD=
����BD=![]()
��Rt��DHB�У�����HBD=30����DB=![]() ��֪��HB=6
��֪��HB=6
����DBF�������������DH��BG����FH=HB=6
��![]() .
.
�ʴ𰸞飺![]() ��
��
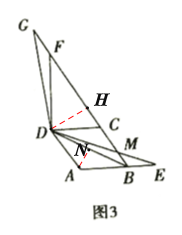



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ�κ���(sh��)y=kx+b��k��0���ĈD��(j��ng)�^(gu��)�c(di��n)A��2��-6�������c����������(sh��)y=-![]() �ĈD�����c(di��n)B��a��4��
�ĈD�����c(di��n)B��a��4��
��1����һ�κ���(sh��)�Ľ���ʽ��
��2����ֱ��AB����ƽ��10��(g��)��λ��õ�ֱ��l��y1=k1x+b1��k1��0����l�c����������(sh��)y2= ![]() �ĈD���ཻ����ʹy1��y2������x��ȡֵ������
�ĈD���ཻ����ʹy1��y2������x��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�̵��M(j��n)��һ����Ʒ�M(j��n)���N(xi��o)�ۣ���(j��ng)�^(gu��)һ��(g��)�µ�ԇ�N(xi��o)�l(f��)�F(xi��n)��ԓ��Ʒ�����N(xi��o)������(r��n)![]() ��Ԫ���c�ۃr(ji��)
��Ԫ���c�ۃr(ji��)![]() ��Ԫ/�����M����κ���(sh��)�P(gu��n)ϵ���@��(g��)�µ��ۃr(ji��)�����N(xi��o)����
��Ԫ/�����M����κ���(sh��)�P(gu��n)ϵ���@��(g��)�µ��ۃr(ji��)�����N(xi��o)����![]() �����������N(xi��o)������(r��n)�ĎM��(du��)��(y��ng)ֵ���±���
�����������N(xi��o)������(r��n)�ĎM��(du��)��(y��ng)ֵ���±���

ע�����N(xi��o)������(r��n)=���N(xi��o)����![]() ���ۃr(ji��)-�M(j��n)�r(ji��)��
���ۃr(ji��)-�M(j��n)�r(ji��)��
��1����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
��2����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)����ʽ��ԓ��Ʒÿ���M(j��n)�r(ji��)�Ƕ���Ԫ��
�ĺ���(sh��)����ʽ��ԓ��Ʒÿ���M(j��n)�r(ji��)�Ƕ���Ԫ��
��3��ԓ��Ʒ�����^�m(x��)�N(xi��o)���@�N��Ʒ����ϣ������1350Ԫ���ϵ����N(xi��o)������(r��n)���ۃr(ji��)��(y��ng)������ʲô������(n��i)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˽�W(xu��)��ÿ���˯����r��ij���ЌW(xu��)У��ȫУ800���W(xu��)�����S�C(j��)��ȡ�˲��W(xu��)�����{(di��o)��������ƽ��ÿ���˯�ߕr(sh��)�g����λ��![]() ���������Ǹ���(j��)�{(di��o)��Y(ji��)���L�ƵĽy(t��ng)Ӌ(j��)�D����һ���֣�
���������Ǹ���(j��)�{(di��o)��Y(ji��)���L�ƵĽy(t��ng)Ӌ(j��)�D����һ���֣�
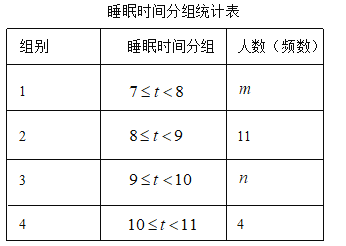
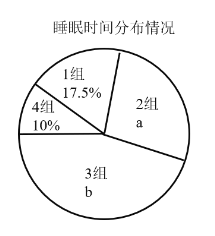
Ո(q��ng)����(j��)������Ϣ��������І�(w��n)�}��
��1�����S�C(j��)��ȡ_______���W(xu��)����
��2��![]() _____��
_____��![]() _______��
_______��![]() ______��
______��![]() ______��
______��
��3����ȡ���@40���W(xu��)��ƽ��ÿ��˯�ߕr(sh��)�g����λ��(sh��)����______�M����M�e����
��4��������ՌW(xu��)УҪ�W(xu��)��ƽ��ÿ���˯�ߕr(sh��)�g��(y��ng)������![]() ��Ո(q��ng)��Ӌ(j��)ԓУ�W(xu��)����˯�ߕr(sh��)�g����Ҫ����˔�(sh��)��
��Ո(q��ng)��Ӌ(j��)ԓУ�W(xu��)����˯�ߕr(sh��)�g����Ҫ����˔�(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
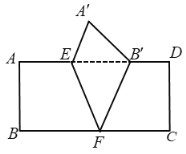
���}Ŀ����D���Ѿ���![]() ��
��![]() ���ۣ��c(di��n)
���ۣ��c(di��n)![]() ǡ������
ǡ������![]() ߅��
߅��![]() ̎����
̎����![]() ��
��![]() ��
��![]() ���t����
���t����![]() ����e�ǣ� ��
����e�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����߅�L(zh��ng)��1��С�����νM�ɵľW(w��ng)���У��o���˸��c(di��n)��߅��ABCD����c(di��n)��W(w��ng)�Ľ��c(di��n)����
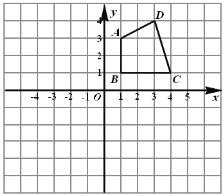
��1����(hu��)����߅��ABCD�P(gu��n)��x�S���S��(du��)�Q����߅��A1B1C1D1��
��2����O��λ�����ģ��ڵ������ޮ�(hu��)����߅��ABCD��λ����߅��A2B2C2D2����λ�ƱȞ�1��
��3���ڵ�һ���ރ�(n��i)�ҳ����c(di��n)P��ʹ��DCP=��CDP������(xi��)���c(di��n)P������(bi��o)����(xi��)��һ��(g��)���ɣ���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���f��˾ÿ������9��00��10��00�鼯�Д������ɼ��r(sh��)�Σ��ׂ}(c��ng)��(k��)�Á�(l��i)���տ�����҂}(c��ng)��(k��)�Á�(l��i)�ɰl(f��)�����ԓ�r(sh��)��(n��i)�ס��҃ɂ}(c��ng)��(k��)�Ŀ����(sh��)��y�������c�r(sh��)�gx���֣�֮�g�ĺ���(sh��)�D����D��ʾ����ô��(d��ng)�ɂ}(c��ng)��(k��)���f����(sh��)��ͬ�r(sh��)���˿̵ĕr(sh��)�g��__________��
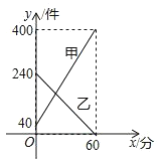
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ��(g��)���M(j��n)ˮ���c��ˮ�ܵ���������ij�r(sh��)���_(k��i)ʼ��![]() ��(n��i)ֻ�M(j��n)ˮ����ˮ�����S���
��(n��i)ֻ�M(j��n)ˮ����ˮ�����S���![]() ��(n��i)���M(j��n)ˮ�ֳ�ˮ��ÿ����M(j��n)ˮ���ͳ�ˮ���ǃɂ�(g��)����(sh��)��������(n��i)��ˮ��
��(n��i)���M(j��n)ˮ�ֳ�ˮ��ÿ����M(j��n)ˮ���ͳ�ˮ���ǃɂ�(g��)����(sh��)��������(n��i)��ˮ��![]() ����λ��
�����![]() ���c�r(sh��)�g
���c�r(sh��)�g![]() �����
����λ��![]() ��֮�g���P(gu��n)ϵ��D��ʾ��
��֮�g���P(gu��n)ϵ��D��ʾ��
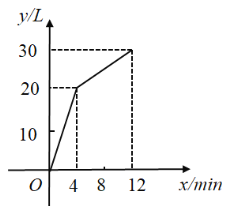
��1����(d��ng)![]() �r(sh��)�����
�r(sh��)�����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
��2��ÿ��犵��M(j��n)ˮ���c��ˮ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D�����タ![]() ��
��![]() �S��
�S��![]() ���c(di��n)����
���c(di��n)����![]() �S���c(di��n)
�S���c(di��n)![]() ֱ��
ֱ��![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() ��
��
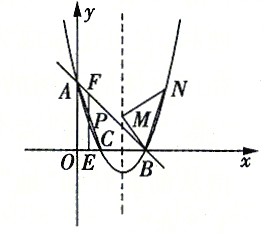
��1�����タ�Ľ���ʽ��
��2���c(di��n)![]() ��ֱ��
��ֱ��![]() �·��Ē��タ��һ��(d��ng)�c(di��n)���^(gu��)�c(di��n)
�·��Ē��タ��һ��(d��ng)�c(di��n)���^(gu��)�c(di��n)![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ��ֱ��
��ֱ��![]() ���c(di��n)
���c(di��n)![]() �O(sh��)�c(di��n)
�O(sh��)�c(di��n)![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��3��![]() �ǵ�һ���ތ�(du��)�Q�S�҂�(c��)���タ�ϵ�һ�c(di��n)���B��
�ǵ�һ���ތ�(du��)�Q�S�҂�(c��)���タ�ϵ�һ�c(di��n)���B��![]() ���タ�Č�(du��)�Q�S���Ƿ�����c(di��n)
���タ�Č�(du��)�Q�S���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() �c
�c![]() ���ƣ���
���ƣ���![]() ��ֱ�ǣ������ڣ�Ո(q��ng)ֱ�ӌ�(xi��)���c(di��n)
��ֱ�ǣ������ڣ�Ո(q��ng)ֱ�ӌ�(xi��)���c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com