Question

1．如圖，在△ABC中，∠BAC=90°，AB=AC，D是AC邊上一動點，CE⊥BD于E．

（1）如圖（1），若BD平分∠ABC時，
①求∠ECD的度數；
②延長CE交BA的延長線于點F，補全圖形，探究BD與EC的數量關系，并證明你的結論；
（2）如圖（2），過點A作AF⊥BE于點F，猜想線段BE，CE，AF之間的數量關系，并證明你的猜想．

Answer 1

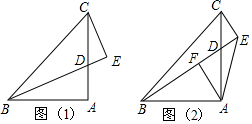
分析 （1）①根據等腰直角三角形的性質得出∠CBA=45°，再利用角平分線的定義解答即可；②延長CE交BA的延長線于點G得出CE=GE，再利用AAS證明△ABD≌△ACG，利用全等三角形的性質解答即可；
（2）過點A作AH⊥AE，交BE于點H，證明△ABH≌△ACE，進而得出CE=BH，利用等腰直角三角形的判定和性質解答即可．

解答 解：（1）①∵在△ABC中，∠BAC=90°，AB=AC，
∴∠CBA=45°，
∵BD平分∠ABC，
∴∠DBA=22.5°，
∵CE⊥BD，
∴∠ECD+∠CDE=90°，∠DBA+∠BDA=90°，
∵∠CDE=∠BDA，
∴∠ECD=∠DBA=22.5°；

②BD=2CE．
證明：延長CE交BA的延長線于點F，如圖1，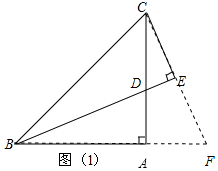
∵BD平分∠ABC，CE⊥BD，
∴CE=FE，
在△ABD與△ACF中，
$\left\{\begin{array}{l}{∠DBA=∠ACF}\\{∠BAC=∠CAF}\\{AB=AC}\end{array}\right.$，
∴△ABD≌△ACF（AAS），
∴BD=CF=2CE；

（2）結論：BE-CE=2AF．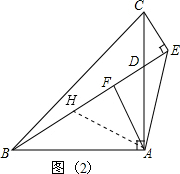
證明：過點A作AH⊥AE，交BE于點H，如圖2，
∵AH⊥AE，
∴∠BAH+∠HAC=∠HAC+∠CAE，
∴∠BAH=∠CAE，
在△ABH與△ACE中，
$\left\{\begin{array}{l}{∠HBA=∠ECA}\\{AB=AC}\\{∠BAH=∠ACE}\end{array}\right.$，
∴△ABH≌△ACE（ASA），
∴CE=BH，AH=AE，
∴△AEH是等腰直角三角形，
∴AF=EF=HF，
∴BE-CE=2AF．

點評 本題屬于三角形綜合題，主要考查的是等腰直角三角形的性質以及全等三角形的判定和性質的綜合應用，作輔助線構造出與所求和已知相關的全等三角形，是解答本題的關鍵．