
| A. | 如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,那么$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 如果|$\overrightarrow{a}$|=|-$\overrightarrow{b}$|,那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C. | 如果$\overrightarrow{a}$∥$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | 如果$\overrightarrow{a}$=-$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
分析 根據向量的定義,可得答案.
解答 解:A、如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$\overline{a}$與$\overline{b}$的大小相等,$\overline{a}$與$\overline{b}$的方向不一向相同,故A錯誤;
B、如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$\overline{a}$與$\overline{b}$的大小相等,$\overline{a}$與$\overline{b}$不一定平行,故B錯誤;
C、如果$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overline{a}$與$\overline{b}$的大小不應定相等,故C錯誤;
D、如果$\overrightarrow{a}$=-$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,故D正確;
故選:D.
點評 本題考查了平面向量,利用向量的定義:既有大小又有方向的量是解題關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 向左平移1個單位,再向上平移2個單位 | |
| B. | 向左平移1個單位,再向下平移2個單位 | |
| C. | 向右平移1個單位,再向上平移2個單位 | |
| D. | 向右平移1個單位,再向下平移2個單位 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6$\sqrt{3}$-2$\sqrt{3}$=4 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{3}$=6$\sqrt{6}$ | D. | 6$\sqrt{2}$÷2$\sqrt{2}$=3$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1200}{x}$-$\frac{1200}{x-40}$=5 | B. | $\frac{1200}{x-40}$-$\frac{1200}{x}$=5 | ||
| C. | $\frac{1200}{x+40}$-$\frac{1200}{x}$=5 | D. | $\frac{1200}{x}$-$\frac{1200}{x+40}$=5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 平均數 | B. | 中位數 | C. | 眾數 | D. | 方差 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
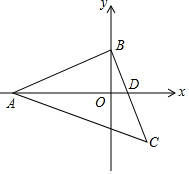 如圖,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),點C在第四象限,BC與x軸交于點D(q,0),x軸恰好平分∠BAC,則點C的坐標為( )
如圖,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),點C在第四象限,BC與x軸交于點D(q,0),x軸恰好平分∠BAC,則點C的坐標為( )| A. | (r,$\frac{p-q}{2}$) | B. | (-$\frac{p}{2}$,$\frac{p-q}{2}$) | C. | (r,p+q) | D. | (2q,$\frac{p-r}{2}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com