
 如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(9,0),(0,4),點D的坐標為(5,0),點P沿矩形的邊C-B-A-O-C運動,當△ODP是腰長為5的等腰三角形時,點P的坐標為(3,4)、(2,4)、(8,4)、(9,3).
如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(9,0),(0,4),點D的坐標為(5,0),點P沿矩形的邊C-B-A-O-C運動,當△ODP是腰長為5的等腰三角形時,點P的坐標為(3,4)、(2,4)、(8,4)、(9,3). 分析 根據當OP=OD時,以及當OD=PD時和當OP=PD時,分別進行討論得出P點的坐標.
解答 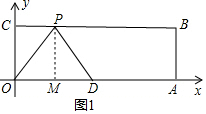 解:①點P在BC邊上運動,過P作PM⊥OA于M.
解:①點P在BC邊上運動,過P作PM⊥OA于M.
(1)如圖1,當OP=OD時,
OP=5,CO=4,
∴易得CP=3,
∴P(3,4);
(2)如圖2,當OD=PD時,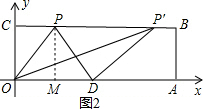
PD=DO=5,PM=4,
∴易得MD=3,從而CP=2或CP′=8,
∴P(2,4)或(8,4);
(3)當OP=PD=5時,OD=6(不合題意舍去),
②如圖3,點P在BA邊上運動,當OD=PD=5時,∵AD=4,∴AP=3,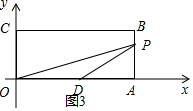
∴P(9,3);
③點P在OA邊上運動,∵O,D,P三點在一條直線上,∴得不到腰長為5的等腰三角形;
④點P在OC邊上運動,∵∠COD=90°,且OC=4<5,∴得不到腰長為5的等腰三角形;
綜上,滿足題意的點P的坐標為(3,4)、(2,4)、(8,4)、(9,3).
故答案為(3,4)、(2,4)、(8,4)、(9,3).
點評 此題主要考查了矩形的性質以及坐標與圖形的性質和等腰三角形的性質,根據△ODP是腰長為5的等腰三角形進行分類討論是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
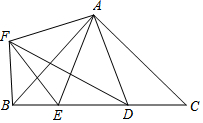 如圖,在Rt△ABC中,AB=AC,D,E是斜邊BC上兩點,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,連接EF.
如圖,在Rt△ABC中,AB=AC,D,E是斜邊BC上兩點,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,連接EF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com