
 如圖,△ABC是等邊三角形,D、E分別為BC、AC上一點,且BD=CE,AD交BE于F.
如圖,△ABC是等邊三角形,D、E分別為BC、AC上一點,且BD=CE,AD交BE于F.分析 (1)根據等邊三角形性質得出AB=BC,∠ABD=∠C=60°,再根據SAS可得△ABD≌△BCE,根據全等三角形的性質得到結論;
(2)由△ABD≌△BCE,可證得∠BAD=∠CBE,進一步得到∠EAF=∠ABE,然后根據有兩角對應相等的三角形相似,即可得△AEF∽△ABE.
解答 解:(1)∵△ABC為等邊三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴AD=BE;
(2)如圖,連接DE,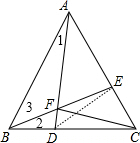
由(1)得:∠1=∠2,
∴∠AFE=∠1+∠3=∠2+∠3=60°,
∵∠ACD=60°,
∴∠AFE=∠ACD,
∵∠FAE=∠CAD,
∴∵△AFE∽△ACD,
∴$\frac{AF}{AC}=\frac{AE}{AD}$,
∴$\frac{AF}{AE}=\frac{AC}{AD}$,
∵∠FAC=∠EAD,
∴△FAC∽△EAD,
∴∠AFC=∠AED,
∵∠AFC=∠AFE+∠CFE=60°+30°=90°,
∴∠AED=90°,
∴CED=90°,
∵∠DCE=60°,
∴∠CDE=30°,
∴CE=$\frac{1}{2}$CD,
∵BD=CE,
∴BD=$\frac{1}{2}$CD,
∴$\frac{BD}{CD}=\frac{1}{2}$.
點評 本題考查了全等三角形的判定和性質,關鍵是根據等邊三角形的性質:等邊三角形的三個內角都相等,且都等于60°;三條邊相等分析.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:初中數學 來源: 題型:填空題
 如圖,正方形ABCD的邊長為6cm,E為CD邊上一點,∠DAE=30°,M為AE的中點,過點M作直線分別與AD、BC相交于點P、Q.若PQ=AE,則AP等于2或4cm.
如圖,正方形ABCD的邊長為6cm,E為CD邊上一點,∠DAE=30°,M為AE的中點,過點M作直線分別與AD、BC相交于點P、Q.若PQ=AE,則AP等于2或4cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知一次函數y1=2x-3與y2=-x+4的圖象相交于點P,它們與y軸交于A、B兩點.
已知一次函數y1=2x-3與y2=-x+4的圖象相交于點P,它們與y軸交于A、B兩點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
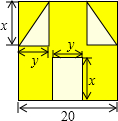 “囧”像一個人臉郁悶的神情.如圖,邊長為a的正方形紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分),設剪去的兩個小直角三角形的兩直角邊長分別為x、y,剪去的小長方形長和寬也分別為x,y.
“囧”像一個人臉郁悶的神情.如圖,邊長為a的正方形紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分),設剪去的兩個小直角三角形的兩直角邊長分別為x、y,剪去的小長方形長和寬也分別為x,y.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在正方形ABCD中,E為BC邊上的點(不與B,C重合),F為CD邊上的點(不與C,D重合),且AE=AF,AB=4,設△AEF的面積為y,EC的長為x,求y關于x的函數關系式,并寫出自變量x的取值范圍.
如圖,在正方形ABCD中,E為BC邊上的點(不與B,C重合),F為CD邊上的點(不與C,D重合),且AE=AF,AB=4,設△AEF的面積為y,EC的長為x,求y關于x的函數關系式,并寫出自變量x的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com