
【題目】如圖,在矩形ABCD中,O為AC中點,EF過O點且EF⊥AC分別交DC于F,交AB于E,若點G是AE中點且∠AOG=30°,則下列結論正確的個數為( )
(1)△OGE是等邊三角形;(2)DC=3OG;(3)OG=![]() BC;(4)S△AOE=
BC;(4)S△AOE=![]() S矩形ABCD
S矩形ABCD
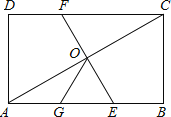
A.1個B.2個C.3個D.4個
【答案】C
【解析】
根據直角三角形斜邊上的中線等于斜邊的一半可得OG=AG=GE=![]() AE,再根據等邊對等角可得∠OAG=30°,根據直角三角形兩銳角互余求出∠GOE=60°,從而判斷出△OGE是等邊三角形,判斷出(1)正確;設AE=2a,根據等邊三角形的性質表示出OE,利用勾股定理列式求出AO,從而得到AC,再求出BC,然后利用勾股定理列式求出AB=3a,從而判斷出(2)正確,(3)錯誤;再根據三角形的面積和矩形的面積列式求出判斷出(4)正確.
AE,再根據等邊對等角可得∠OAG=30°,根據直角三角形兩銳角互余求出∠GOE=60°,從而判斷出△OGE是等邊三角形,判斷出(1)正確;設AE=2a,根據等邊三角形的性質表示出OE,利用勾股定理列式求出AO,從而得到AC,再求出BC,然后利用勾股定理列式求出AB=3a,從而判斷出(2)正確,(3)錯誤;再根據三角形的面積和矩形的面積列式求出判斷出(4)正確.
解:∵EF⊥AC,點G是AE中點,
∴OG=AG=GE=![]() AE,
AE,
∵∠AOG=30°,
∴∠OAG=∠AOG=30°,
∠GOE=90°﹣∠AOG=90°﹣30°=60°,
∴△OGE是等邊三角形,故(1)正確;
設AE=2a,則OE=OG=a,
由勾股定理得,AO=![]() =
=![]() =
=![]() a,
a,
∵O為AC中點,
∴AC=2AO=2![]() a,
a,
∴BC=![]() AC=
AC=![]() ×2
×2![]() a=
a=![]() a,
a,
在Rt△ABC中,由勾股定理得,AB=![]() =3a,
=3a,
∵四邊形ABCD是矩形,
∴CD=AB=3a,
∴DC=3OG,故(2)正確;
∵OG=a,![]() BC=
BC=![]() a,
a,
∴OG≠![]() BC,故(3)錯誤;
BC,故(3)錯誤;
∵S△AOE=![]() a
a![]() a=
a=![]() a2,
a2,
SABCD=3a![]() a=3
a=3![]() a2,
a2,
∴S△AOE=![]() SABCD,故(4)正確;
SABCD,故(4)正確;
綜上所述,結論正確是(1)(2)(4),共3個.
故選:C.


科目:初中數學 來源: 題型:
【題目】某養殖戶每年的養殖成本包括固定成本和可變成本,其中固定成本每年均為4萬元,可變成本逐年增長,已知該養殖戶第一年的可變成本為2.6萬元,設可變成本平均每年增長的百分率為![]()
(1)用含x的代數式表示低3年的可變成本為 萬元;
(2)如果該養殖戶第3年的養殖成本為7.146萬元,求可變成本平均每年的增長百分率x.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三(1)班50名學生需要參加體育“五選一”自選項目測試,小明根據班上學生所報自選項目的情況繪制了統計圖如下:
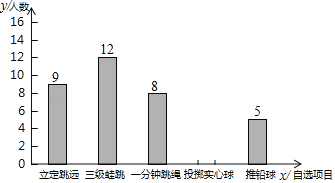
(1)補全條形統計圖;
(2)若將各自選項的人數所占比例繪制成扇形統計圖,求“三級蛙跳”對應扇形的圓心角的度數;
(3)在選報“推鉛球”的學生中,有3名男生,2名女生,為了了解學生的訓練效果,從這5名學生中隨機抽取2名學生進行推鉛球測試,求所抽取的兩名學生中至少有一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4![]() ,點D是AC邊上一動點,連接BD,以AD為直徑的圓交BD于點E,則線段CE長度的最小值為___.
,點D是AC邊上一動點,連接BD,以AD為直徑的圓交BD于點E,則線段CE長度的最小值為___.
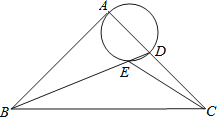
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系中,△ABC是直角三角形,∠ACB=90°,點A,C的坐標分別為A(﹣3,0),C(1,0),BC=![]() AC
AC
(1)求過點A,B的直線的函數表達式;
(2)在x軸上找一點D,連接DB,使得△ADB與△ABC相似(不包括全等),并求點D的坐標;
(3)在(2)的條件下,如P,Q分別是AB和AD上的動點,連接PQ,設AP=DQ=m,問是否存在這樣的m,使得△APQ與△ADB相似?如存在,請求出m的值;如不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 于點
于點![]() . 點
. 點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向點
向點![]() 運動,點
運動,點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向點
向點![]() 運動,兩點同時出發,速度都為每秒1個單位長度,當點
運動,兩點同時出發,速度都為每秒1個單位長度,當點![]() 運動到
運動到![]() 時,兩點都停止. 設運動時間為
時,兩點都停止. 設運動時間為![]() 秒.
秒.
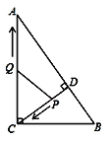
(1)求線段![]() 的長;
的長;
(2)當![]() 為何值時,
為何值時,![]() 是直角三角形?
是直角三角形?
(3)是否存在某一時刻,使得![]() 分
分![]() 的面積為1:11?若存在,求出
的面積為1:11?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】方方駕駛小汽車勻速地從A地行使到B地,行駛里程為480千米,設小汽車的行使時間為t(單位:小時),行使速度為v(單位:千米/小時),且全程速度限定為不超過120千米/小時.
⑴求v關于t的函數表達式;
⑵方方上午8點駕駛小汽車從A出發.
①方方需在當天12點48分至14點(含12點48分和14點)間到達B地,求小汽車行駛速度v的范圍.
②方方能否在當天11點30分前到達B地?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com