
 如圖,△ABC中,E、F分別是AB、AC上的兩點,且$\frac{AE}{EB}=\frac{AF}{FC}=\frac{1}{2}$,若△AEF的面積為3,則四邊形EBCF的面積為24.
如圖,△ABC中,E、F分別是AB、AC上的兩點,且$\frac{AE}{EB}=\frac{AF}{FC}=\frac{1}{2}$,若△AEF的面積為3,則四邊形EBCF的面積為24. 分析 根據題意可判定△AEF∽△ABC,利用面積比等于相似比平方可得出△ABC的面積,繼而根據S四邊形EBCF=S△ABC-S△AEF,即可得出答案.
解答 解:∵$\frac{AE}{EB}=\frac{AF}{FC}=\frac{1}{2}$,
∴EF∥BC,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2=($\frac{1}{3}$)2=$\frac{1}{9}$,
∴S△ABC=27,
則S四邊形EBCF=S△ABC-S△AEF=27-3=24.
故答案為:24.
點評 本題考查了相似三角形的判定與性質,解答本題的關鍵是證明△AEF∽△ABC,要求同學們熟練掌握相似三角形的面積比等于相似比平方.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
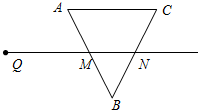 如圖,射線QN與邊長為8的等邊△ABC的兩邊AB,BC分別交于點M,N,且AC∥QN.動點P從點Q出發,沿射線QN以每秒2cm的速度向右移動,以點P為圓心,2$\sqrt{3}$cm為半徑的圓也隨之移動.若AM=MB=4cm,QM=8cm,且經過t秒,當⊙P與△ABC的邊相切時,則t可取的一切值為t=2或3≤t≤7或t=8(單位:秒).
如圖,射線QN與邊長為8的等邊△ABC的兩邊AB,BC分別交于點M,N,且AC∥QN.動點P從點Q出發,沿射線QN以每秒2cm的速度向右移動,以點P為圓心,2$\sqrt{3}$cm為半徑的圓也隨之移動.若AM=MB=4cm,QM=8cm,且經過t秒,當⊙P與△ABC的邊相切時,則t可取的一切值為t=2或3≤t≤7或t=8(單位:秒).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
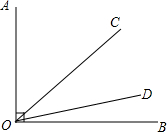 如圖,已知∠AOB=90°,射線OC繞點O從OA位置開始,以每秒4°的速度順時針方向旋轉;同時,射線OD繞點O從OB位置開始,以每秒1°的速度逆時針方向旋轉.當OC與OA成180°時,OC與OD同時停止旋轉.
如圖,已知∠AOB=90°,射線OC繞點O從OA位置開始,以每秒4°的速度順時針方向旋轉;同時,射線OD繞點O從OB位置開始,以每秒1°的速度逆時針方向旋轉.當OC與OA成180°時,OC與OD同時停止旋轉.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com