
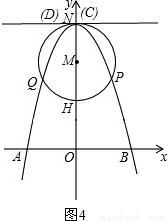
已知過原點O的兩直線與圓心為M(0,4),半徑為2的圓相切,切點分別為P、Q,PQ交y軸于點K,拋物線經過P、Q兩點,頂點為N(0,6),且與x軸交于A、B兩點.

(1)求點P的坐標;
(2)求拋物線解析式;
(3)在直線y=nx+m中,當n=0,m≠0時,y=m是平行于x軸的直線,設直線y=m與拋物線相交于點C、D,當該直線與⊙M相切時,求點A、B、C、D圍成的多邊形的面積(結果保留根號).
(1)點P的坐標為(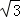 ,3) (2)
,3) (2)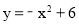 (3)4+2
(3)4+2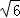 或6
或6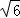
【解析】
試題分析:(1)由切線的性質可得∠MPO=90°,根據勾股定理可求出PO,然后由面積法可求出PK,然后運用勾股定理可求出OK,就可得到點P的坐標;
(2)可設頂點為(0,6)的拋物線的解析式為y=ax2+6,然后將點P的坐標代入就可求出拋物線的解析式;(3)直線y=m與⊙M相切有兩種可能,只需對這兩種情況分別討論就可求出對應多邊形的面積.
試題解析:【解析】
(1)如圖1,
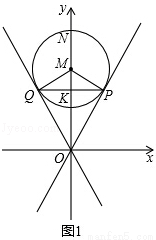
∵⊙M與OP相切于點P,
∴MP⊥OP,即∠MPO=90°.
∵點M(0,4)即OM=4,MP=2,
∴OP=2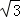 .
.
∵⊙M與OP相切于點P,⊙M與OQ相切于點Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=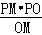 =
=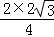 =
=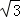 .
.
∴OK=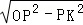 =3.
=3.
∴點P的坐標為(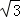 ,3).
,3).
(2)如圖2,
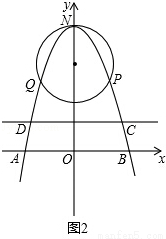
設頂點為(0,6)的拋物線的解析式為y=ax2+6,
∵點P(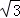 ,3)在拋物線y=ax2+6上,
,3)在拋物線y=ax2+6上,
∴3a+6=3.
解得:a=﹣1.
則該拋物線的解析式為y=﹣x2+6.
(3)當直線y=m與⊙M相切時,
則有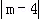 =2.
=2.
解得;m1=2,m2=6.
①m=2時,如圖3,
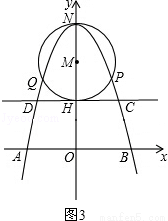
則有OH=2.
當y=2時,解方程﹣x2+6=2得:x=±2,
則點C(2,2),D(﹣2,2),CD=4.
同理可得:AB=2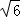 .
.
則S梯形ABCD= (DC+AB)•OH=
(DC+AB)•OH= (4+2
(4+2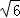 )×2=4+2
)×2=4+2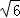 .
.
②m=6時,如圖4,
此時點C、點D與點N重合.
S△ABC=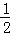 AB•OC=
AB•OC=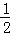 ×2
×2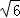 ×6=6
×6=6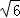 .
.
綜上所述:點A、B、C、D圍成的多邊形的面積為4+2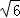 或6
或6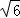
考點:切線的性質,勾股定理,二次函數的圖像與性質,梯形及三角形的面積


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源:[同步]2014年北師大版八年級上 2.5用計算器開方練習卷(解析版) 題型:?????
用計算器計算,若按鍵順序為 ,相應算式是( )
,相應算式是( )
A. ×5﹣0×5÷2= B.(
×5﹣0×5÷2= B.( ×5﹣0×5)÷2=
×5﹣0×5)÷2=
C. ﹣0•5÷2= D.(
﹣0•5÷2= D.( =0•5)÷2=
=0•5)÷2=
查看答案和解析>>
科目:初中數學 來源:[同步]2014年北師大版八年級上 2.4估算練習卷(解析版) 題型:?????
(2014•日照)在已知實數:﹣1,0,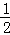 ,﹣2中,最小的一個實數是( )
,﹣2中,最小的一個實數是( )
A.﹣1 B.0 C.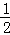 D.﹣2
D.﹣2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省溫州市五校聯賽九年級實驗B班1月聯考數學試卷(解析版) 題型:選擇題
在半徑為2的圓中,弦AB的長為2,則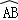 的長等于( )
的長等于( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省臺州市九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,直線y=x+m和拋物線y=x2+bx+c都經過點A(1,0),B(3,2).
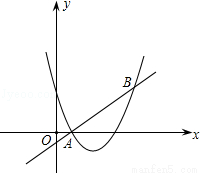
(1)求m的值和拋物線的解析式;(8分)
(2)求不等式x2+bx+c>x+m的解集.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省臺州市九年級上學期期中考試數學試卷(解析版) 題型:填空題
若關于x的一元二次方程kx2+4x+3=0有實根,則k的非負整數值是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省張家港市九年級上學期第三次階段性測試數學試卷(解析版) 題型:解答題
(本題滿分8分)已知拋物線y= +kx+b經過點P(2,-3),Q(-1,0).
+kx+b經過點P(2,-3),Q(-1,0).

(1)求拋物線的解析式.
(2)設拋物線頂點為 ,與
,與 軸交點為
軸交點為 .求
.求 的值.
的值.
(3)設拋物線與 軸的另一個交點為
軸的另一個交點為 ,求四邊形
,求四邊形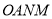 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省蘇州市九年級12月月考數學試卷(解析版) 題型:填空題
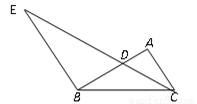
如圖,點D為△ABC的邊AB上的一點,連結CD,過點B作BE//AC交CD的延長線于點E,且∠ACD=∠DBC,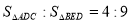 ,AB=10,則AC的長為
,AB=10,則AC的長為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com