
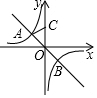
 如圖,直線y=-x與雙曲線y=-$\frac{2}{x}$相交于點A,B,點C在y軸的正半軸上,且OC=OB,則△AOC的面積為( )
如圖,直線y=-x與雙曲線y=-$\frac{2}{x}$相交于點A,B,點C在y軸的正半軸上,且OC=OB,則△AOC的面積為( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
分析 聯立正、反比例函數解析式成方程組,解之可求出點A、B的坐標,進而可得出OB=2,再根據OC=OB結合三角形的面積公式即可得出結論.
解答 解:聯立正、反比例函數解析式成方程組,
$\left\{\begin{array}{l}{y=-x}\\{y=-\frac{2}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-\sqrt{2}}\\{{y}_{1}=\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{2}}\\{{y}_{2}=-\sqrt{2}}\end{array}\right.$,
∴點A的坐標為(-$\sqrt{2}$,$\sqrt{2}$),點B的坐標為($\sqrt{2}$,-$\sqrt{2}$).
∴OB=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2.
∵OC=OB,
∴S△AOC=$\frac{1}{2}$OC•|xA|=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$.
故選D.
點評 本題考查了反比例函數與一次函數的交點問題以及三角形的面積,聯立正、反比例函數解析式成方程組求出兩函數圖象的交點坐標是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
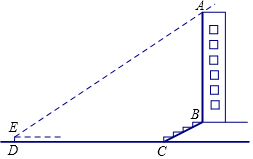 某校興趣小組想測量一座大樓AB的高度.如圖,大樓前有一段斜坡BC,已知BC的長為12米,它的坡度i=1:$\sqrt{3}$.在離C點40米的D處,用測角儀測得大樓頂端A的仰角為37°,測角儀DE的高為1.5米,求大樓AB的高度約為多少米?(結果精確到0.1米)
某校興趣小組想測量一座大樓AB的高度.如圖,大樓前有一段斜坡BC,已知BC的長為12米,它的坡度i=1:$\sqrt{3}$.在離C點40米的D處,用測角儀測得大樓頂端A的仰角為37°,測角儀DE的高為1.5米,求大樓AB的高度約為多少米?(結果精確到0.1米)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
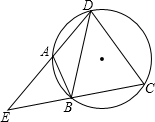 如圖,點A、B、C、D在同一個圓上,DB=DC,DA、CB的延長線相交于點E,若∠BDC=a,則∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)
如圖,點A、B、C、D在同一個圓上,DB=DC,DA、CB的延長線相交于點E,若∠BDC=a,則∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
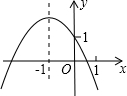 已知二次函數y=ax2+bx+c的圖象如圖所示,有以下結論:
已知二次函數y=ax2+bx+c的圖象如圖所示,有以下結論:| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖是由若干個邊長為1個單位長度的小正方形組成的網格圖,已知四邊形ABCD在網圖的格點上.按要求完成下列各小題.
如圖是由若干個邊長為1個單位長度的小正方形組成的網格圖,已知四邊形ABCD在網圖的格點上.按要求完成下列各小題.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com