
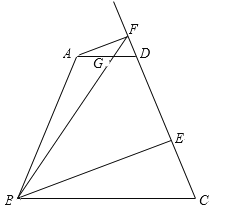
【題目】如圖,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,![]() .E為射線CD上任意一點,過點A作AF // BE,與射線CD相交于點F.聯結BF,與直線AD相交于點G.設CE = x,
.E為射線CD上任意一點,過點A作AF // BE,與射線CD相交于點F.聯結BF,與直線AD相交于點G.設CE = x,![]() .
.
(1)求AB的長;
(2)當點G在線段AD上時,求y關于x的函數解析式,并寫出函數的定義域;
(3)如果![]() ,求線段CE的長.
,求線段CE的長.
【答案】(1)AB = 13;(2)所求函數的解析式為![]() ,函數定義域為
,函數定義域為![]() ;(3)如果點G在邊AD上,
;(3)如果點G在邊AD上,![]() ;如果點G在邊DA的延長線上,
;如果點G在邊DA的延長線上,![]() .
.
【解析】
(1)分別過點A、D作AM⊥BC、DN⊥BC,垂足為點M、N,根據三角函數解答即可;
(2)根據相似三角形的判定和性質解答,進而利用函數解析式解答即可;
(3)根據兩種情況,利用勾股定理解答即可.
解:(1)分別過點A、D作AM⊥BC、DN⊥BC,垂足為點M、N.
∵AD//BC,AB=CD,AD=5,BC=15,
∴![]() .
.
在Rt△ABM中,∠AMB=90°,
∴![]() .
.
∴AB=13.
(2)∵![]() ,∴
,∴![]() .即得
.即得![]() .
.
∵∠AFD=∠BEC,∠ADF=∠C.∴△ADF∽△BCE.
∴![]() .
.
又∵CE=x,![]() ,AB=CD=13.即得
,AB=CD=13.即得![]() .
.
∵AD//BC,∴![]() .∴
.∴ .
.
∴![]() .
.
∴所求函數的解析式為![]() ,函數定義域為
,函數定義域為![]() .
.
(3)在Rt△ABM中,利用勾股定理,得![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
設![]() .由△ADF∽△BCE,
.由△ADF∽△BCE,![]() ,得
,得![]() .
.
過點E作EH⊥BC,垂足為點H.
由題意,本題有兩種情況:
(ⅰ)如果點G在邊AD上,則![]() .
.
∴S=5.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由DN⊥BC,EH⊥BC,易得EH//DN.
∴![]() .
.
又CD=AB=13,∴![]() .
.
(2)如果點G在邊DA的延長線上,則![]() .
.
∴![]() .解得
.解得![]() .
.
∴![]() .
.
∴![]() .解得
.解得![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.


科目:初中數學 來源: 題型:
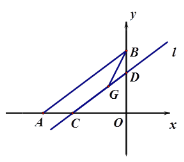
【題目】如圖,已知A(-4,0)、B(0,3),一次函數![]() 與坐標軸分別交于C、D兩點,G為CD上一點,且DG:CG=1:2,連接BG,當BG平分∠ABO時,則b的值為____.
與坐標軸分別交于C、D兩點,G為CD上一點,且DG:CG=1:2,連接BG,當BG平分∠ABO時,則b的值為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中裝有標著數字2,3,4,5的4個小球,這4個小球的材質、大小和形狀完全相同,現從中隨機摸出兩個小球,這兩個小球上的數字之積大于9的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙、丁兩位同學做傳球游戲:第一次由甲將球隨機傳給乙、丙、丁中的某一人,從第二次起,每一次都由持球者將球再隨機傳給其他三人中的某一人,則第二次傳球后球回到甲手里的概率是________;第三次傳球后球回到甲手里的概率是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
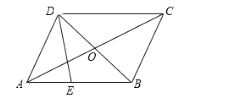
【題目】如圖,在平行四邊形ABCD中,對角線AC、BD相交于點O.E為邊AB上一點,且BE = 2AE.設![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果點F是線段OC的中點,那么向量![]() ,并在圖中畫出向量
,并在圖中畫出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本題結果用向量![]() 的式子表示.畫圖不要求寫作法,但要指出所作圖中表示結論的向量.
的式子表示.畫圖不要求寫作法,但要指出所作圖中表示結論的向量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是⊙O的圓內接四邊形,線段AB是⊙O的直徑,連結AC.BD.點H是線段BD上的一點,連結AH、CH,且∠ACH=∠CBD,AD=CH,BA的延長線與CD的延長線相交與點P.
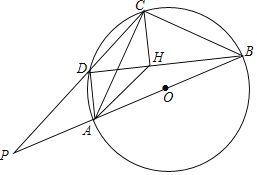
(1)求證:四邊形ADCH是平行四邊形;
(2)若AC=BC,PB=![]() PD,AB+CD=2(
PD,AB+CD=2(![]() +1)
+1)
①求證:△DHC為等腰直角三角形;②求CH的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市居民用水實行以戶為單位的三級階梯收費辦法:
第一級:居民每戶每月用水![]() 噸以內含
噸以內含![]() 噸,每噸收水費
噸,每噸收水費![]() 元;
元;
第二級:居民每戶每月用水超過![]() 噸但不超過
噸但不超過![]() 噸,未超過
噸,未超過![]() 的部分按照第一級標準收費,超過部分每噸收水費
的部分按照第一級標準收費,超過部分每噸收水費![]() 元;
元;
第三級:居民每戶每月用水超過![]() 噸,未超過
噸,未超過![]() 噸的部分按照第一、二級標準收費,超過部分每噸收水費
噸的部分按照第一、二級標準收費,超過部分每噸收水費![]() 元;
元;
設一戶居民月用水![]() 噸,應繳水費
噸,應繳水費![]() 元,
元,![]() 與
與![]() 之間的函數關系如圖所示,
之間的函數關系如圖所示,
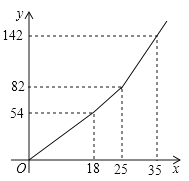
(Ⅰ)根據圖象直接作答:![]() ___________,
___________,![]() _______________,
_______________,![]() _______________;
_______________;
(Ⅱ)求當![]() 時,
時,![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(Ⅲ)把上述水費階梯收費辦法稱為方案①,假設還存在方案②;居民每戶月用水一律按照每噸![]() 元的標準繳費.當居民用戶月用水超過
元的標準繳費.當居民用戶月用水超過![]() 噸時,請你根據居民每戶月用水量的大小設計出對居民繳費最實惠的方案.
噸時,請你根據居民每戶月用水量的大小設計出對居民繳費最實惠的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
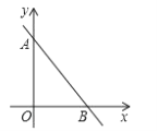
【題目】如圖,在直角坐標系xOy中,O為坐標原點,直線AB分別與y軸,x軸交于A(0,4),B(3,0)兩點.
(1)尺規作圖:在x軸上求作一點C,使得△ABC是以![]() 為頂角的等腰三角形,并在圖中標明相應字母;(保留作圖痕跡,不寫作法)
為頂角的等腰三角形,并在圖中標明相應字母;(保留作圖痕跡,不寫作法)
(2)在(1)的條件下,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是矩形ABCD的邊AD的中點,且BE⊥AC于點F,則下列結論中錯誤的是( )
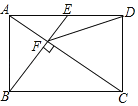
A.AF=![]() CF
CF
B.∠DCF=∠DFC
C.圖中與△AEF相似的三角形共有5個
D.tan∠CAD=![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com