
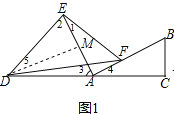
【題目】如圖1所示,在Rt△ABC中,∠C=90°,點D是線段CA延長線上一點,且AD=AB.點F是線段AB上一點,連接DF,以DF為斜邊作等腰Rt△DFE,連接EA,EA滿足條件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的長度;
(2)求證:AE=AF+BC;
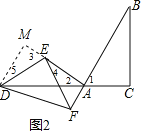
(3)如圖2,點F是線段BA延長線上一點,探究AE、AF、BC之間的數量關系,并證明.
【答案】(1)![]() (2)證明見解析;(3)AE+AF=BC,證明見解析
(2)證明見解析;(3)AE+AF=BC,證明見解析
【解析】
試題分析:(1)在等腰直角三角形DEF中,∠DEF=90°,求得∠1=20°,根據余角的定義得到∠2=∠DEF﹣∠1=70°,根據三角形的內角和得到∠3=60°,∠4=30°根據三角函數的定義得到cos∠4=![]() ,于是得到結論;
,于是得到結論;
(2)如圖1,過D作DM⊥AE于D,在△DEM中,由余角的定義得到∠2+∠5=90°,由于∠2+∠1=90°,推出∠1=∠5證得△DEM≌△EFA,根據全等三角形的性質得到AF=EM,根據三角形的內角和和余角的定義得到∠3=∠B,推出△DAM≌△ABC,根據全等三角形的性質得到BC=AM即可得到結論;
(3)如圖2,過D作DM⊥AE交AE的延長線于M根據余角的定義和三角形的內角和得到∠2=∠B,證得△ADM≌△BAC,由全等三角形的性質得到BC=AM,由于EF=DE,∠DEF=90°,推出∠4=∠5,證得△MED≌△AFE,根據全等三角形的性質得到ME=AF,即可得到結論.
解:(1)在等腰直角三角形DEF中,∠DEF=90°,
∵∠1=20°,
∴∠2=∠DEF﹣∠1=70°,
∵∠EDA+∠2+∠3=180°,
∴∠3=60°,
∵EA⊥AB,
∴∠EAB=90°,
∵∠3+∠EAB+∠A=180°,
∴∠4=30°,
∵∠C=90°,
∴cos∠4=![]() ,
,
∴AB=![]() =
=![]() =
=![]() ;
;
(2)如圖1,過D作DM⊥AE于D,在△DEM中,∠2+∠5=90°,
∵∠2+∠1=90°,
∴∠1=∠5,
∵DE=FE,
在△DEM與△EFA中,
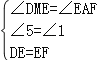 ,
,
∴△DEM≌△EFA,
∴AF=EM,
∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,
∴∠3+∠4=90°,
∴∠3=∠B,
在△DAM與△ABC中,
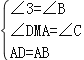 ,
,
∴△DAM≌△ABC,
∴BC=AM,
∴AE=EM+AM=AF+BC;
(3)如圖2,過D作DM⊥AE交AE的延長線于M,
∵∠C=90°,
∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,
∴∠2+∠1=90°,∠2=∠B,
在△ADM與△BAC中,
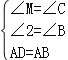 ,
,
∴△ADM≌△BAC,
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠3+∠DEF+∠4=180°,
∴∠3+∠4=90°,
∵∠3+∠5=90°,
∴∠4=∠5,
在△MED與△AFE中,
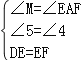 ,
,
∴△MED≌△AFE,
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.


科目:初中數學 來源: 題型:
【題目】家庭過期藥品屬于“國家危險廢物“處理不當將污染環境,危害健康.某市藥監部門為了了解市民家庭處理過期藥品的方式,決定對全市家庭作一次簡單隨機抽樣調查本次抽樣調查發現,接受調查的家庭都有過期藥品,現將有關數據呈現如圖:
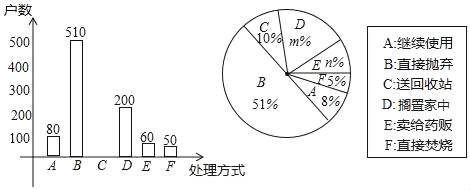
(1)求m、n的值;
(2)補全條形統計圖;
(3)家庭過期藥品的正確處理方式是送回收站,若該市有180萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收站.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數列:0,2,4,8,12,18,…是我國的大衍數列,也是世界數學史上第一道數列題.該數列中的奇數項可表示為![]() ,偶數項表示為
,偶數項表示為![]() .
.
如:第一個數為![]() =0,第二個數為
=0,第二個數為![]() =2,…
=2,…
現在數軸的原點上有一點P,依次以大衍數列中的數為距離向左右來回跳躍.
第1秒時,點P在原點,記為P1;
第2秒時,點P向左跳2個單位,記為P2,此時點P2所表示的數為-2;
第3秒時,點P向右跳4個單位,記為P3,此時點P3所表示的數為2;
…
按此規律跳躍,點P20表示的數為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上兩點A,B對應的數分別為-4,8.
(1)如圖1,如果點P和點Q分別從點A,點B同時出發,沿數軸負方向運動,點P的運動速度為每秒2個單位,點Q的運動速度為每秒6個單位.
① 求A,B兩點之間的距離.
② 當P,Q兩點相遇時,點P在數軸上對應的數幾.
③ 求點P出發多少秒后,與點Q之間相距4個單位長度?
(2)如圖2,如果點P從點A出發沿數軸的正方向以每秒2個單位的速度運動,點Q從點B出發沿數軸的負方向以每秒6個單位的速度運動,點M從數軸原點O出發沿數軸的正方向以每秒1個單位的速度運動,若三個點同時出發,經過多少秒后有MP=MQ?
![]()
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作等邊△ABC和等邊△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正確的結論的個數是( )
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A在第二象限內,點B在x軸上,∠AOB=30°,AB=BO,反比例函數y= ![]() (x<0)的圖象經過點A,若S△ABO=
(x<0)的圖象經過點A,若S△ABO= ![]() ,則k的值為 .
,則k的值為 . 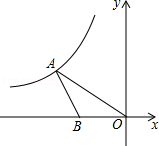
查看答案和解析>>
科目:初中數學 來源: 題型:
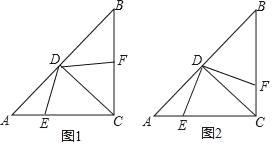
【題目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分線,點E,F分別是邊AC, BC上的動點,AC=4,設AE=x,BF=y.
(1)若x+y=3,求四邊形CEDF的面積;
(2)當DE⊥DF時,如圖2,試探索x、y之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
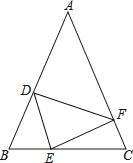
【題目】如圖,在△ABC中,AB=AC,點D,E,F分別在AB,BC,AC邊上,且BE=CF,BD=CE.
(1)求證:△DEF是等腰三角形;
(2)當∠A=50°時,求∠DEF的度數;
(3)若∠A=∠DEF,判斷△DEF是否為等腰直角三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com