
【題目】如圖,已知![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )求證:
)求證: ![]() ≌
≌![]() .
.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的長.
的長.

【答案】(![]() )證明見解析;(
)證明見解析;(![]() )
)![]() .
.
【解析】試題分析:(1)已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,根據角平分線的性質定理可得CE=CF,再由![]() ,根據HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL證明Rt△AFC≌△Rt△AEC,即可得AE=AF,設DF=x,則有9+x=21-x,得x=6,在Rt△CDF中,根據勾股定理求得CF=8,在Rt△AFC中,再運用勾股定理求得AC即可.
,根據HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL證明Rt△AFC≌△Rt△AEC,即可得AE=AF,設DF=x,則有9+x=21-x,得x=6,在Rt△CDF中,根據勾股定理求得CF=8,在Rt△AFC中,再運用勾股定理求得AC即可.
試題解析:
(![]() )證明:∵
)證明:∵![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() .
.
(![]() )由(
)由(![]() )得,
)得, ![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() 與
與![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
設![]() ,則有
,則有![]() ,得
,得![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】已知一次函數y=2x+4
(1)在如圖所示的平面直角坐標系中,畫出函數的圖象;

2)求圖象與x軸的交點A的坐標,與y軸交點B的坐標;
(3)在(2)的條件下,求出△AOB的面積;
(4)利用圖象直接寫出:當y<0時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在寬為20m,長為32m的矩形地面上修筑同樣寬的道路(圖中陰影部分),余下的部分種上草坪.要使草坪的面積為540m2,求道路的寬.
(部分參考數據:322=1024,522=2704,482=2304)

查看答案和解析>>
科目:初中數學 來源: 題型:
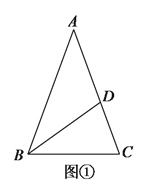
【題目】(![]() )如圖①,在
)如圖①,在![]() 中,
中,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度數.
的度數.
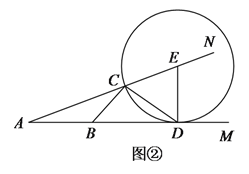
(![]() )如圖②,點
)如圖②,點![]() ,
,![]() 在射線
在射線![]() 上,點
上,點![]() ,
,![]() 在射線
在射線![]() 上,且
上,且![]() .
.
①若![]() ,求
,求![]() 的度數.
的度數.
②若以![]() 為圓心,
為圓心,![]() 為半徑作弧,與射線
為半徑作弧,與射線![]() 上沒有交點(除
上沒有交點(除![]() 點外),直接寫出
點外),直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1在正方形ABCD的外側作兩個等邊三角形ADE和DCF,連接AF,BE.

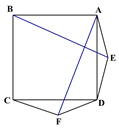

(圖1) (圖2) (備用圖)
(1)請判斷:AF與BE的數量關系是_____________,位置關系______________;
(2)如圖2,若將條件“兩個等邊三角形ADE和DCF”變為“兩個等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)問中的結論是否仍然成立?請作出判斷并給予證明;
(3)若三角形ADE和DCF為一般三角形,且AE=DF,ED=FC,第(1)問中的結論都能成立嗎?請直接寫出你的判斷.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新農村社區改造中,有一部分樓盤要對外銷售,某樓盤共23層,銷售價格如下:第八層樓房售價為4000元/米2,從第八層起每上升一層,每平方米的售價提高50元;反之,樓層每下降一層,每平方米的售價降低30元,已知該樓盤每套樓房面積均為120米2.
若購買者一次性付清所有房款,開發商有兩種優惠方案:
方案一:降價8%,另外每套樓房贈送a元裝修基金;
方案二:降價10%,沒有其他贈送.
(1)請寫出售價y(元/米2)與樓層x(1≤x≤23,x取整數)之間的函數關系式;
(2)老王要購買第十六層的一套樓房,若他一次性付清購房款,請幫他計算哪種優惠方案更加合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛客車從甲地開往乙地,一輛轎車從乙地開往甲地,兩車同時出發,兩車行駛x小時后,記客車離甲地的距離為y1千米,轎車離甲地的距離為y2千米,y1、y2關于x的函數圖象如圖.
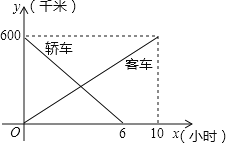
(1)根據圖象,直接寫出y1、y2關于x的函數關系式;
(2)當兩車相遇時,求此時客車行駛的時間;
(3)兩車相距200千米時,求客車行駛的時間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com