
【題目】![]() 中,
中,![]() ,以
,以![]() 為直徑的
為直徑的![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,點
,點![]() 為
為![]() 延長線上的一點,
延長線上的一點,![]() 延長交
延長交![]() 于
于![]() ,
,![]() .小華得出
.小華得出![]() 個結論:①
個結論:①![]() ;②
;②![]() ;③
;③![]() .
.
其中正確的是( )

A. ①② B. ①③ C. ②③ D. ①②③
【答案】D
【解析】
首先連接OE,CE,由OE=OD,PE=PF,易得∠OED+∠PEF=∠ODE+∠PFE,又由OD⊥BC,可得OE⊥PE,繼而證得PE為⊙O的切線;
又由BC是直徑,可得CE⊥AB,由切線長定理可得GC=GE,根據等角的余角相等,可得∠A=∠AEG,根據等腰三角形的判定,可得答案;
易證得OG是△ABC的中位線,則可得OG∥BE.
連接OE,CE.
∵OE=OD,PE=PF,∴∠OED=∠ODE,∠PEF=∠PFE.
∵OD⊥BC,∴∠ODE+∠OFD=90°.
∵∠OFD=∠PFE,∴∠OED+∠PEF=90°,即OE⊥PE.
∵點E在⊙O上,∴GE為⊙O的切線;
點C在⊙O上,OC⊥GC,∴GC為⊙O的切線,∴GC=GE.
故①正確;
∵BC是直徑,∴∠BEC=90°,∴∠AEC=90°.
∵∠ACB=90°,∴AC是⊙O的切線,∴EG=CG,∴∠GCE=∠GEC.
∵∠GCE+∠A=90°,∠GEC+∠AEG=90°,∴∠A=∠AEG,∴AG=EG;故②正確;
∵OC=OB,AG=CG,∴OG是△ABC的中位線,∴OG∥AB;故③正確.
故選D.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】一個尋寶游戲的尋寶通道如圖①所示,通道由在同一平面內的AB,BC,CA,OA, OB,OC組成。為記錄尋寶者的行進路線,在BC的中點M處放置了一臺定位儀器,設尋寶者行進的時間為x,尋寶者與定位儀器之間的距離為y,若尋寶者勻速行進,且表示y與x的函數關系的圖像大致如圖②所示,則尋寶者的行進路線可能為:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,直線y=﹣x+3與x軸、y軸交于點A,點B,點O關于直線AB的對稱點為點O′,且點O′恰好在反比例函數y=![]() 的圖象上.
的圖象上.
(1)求點A與B的坐標;
(2)求k的值;
(3)若y軸正半軸有點P,過點P作x軸的平行線,且與反比例函數y=![]() 的圖象交于點Q,設A、P、Q、O′四個點所圍成的四邊形的面積為S.若S=
的圖象交于點Q,設A、P、Q、O′四個點所圍成的四邊形的面積為S.若S=![]() S△OAB時,求點P的坐標.
S△OAB時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=AC,AC的垂直平分線MN交AB于D,交AC于E.

(1)若∠A=40°,求∠BCD的度數;
(2)若AE=5,△BCD的周長17,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖,在平面直角坐標系中,點A的坐標為(0,4),點B的坐標為(3,0),

(1)在圖中作出線段AB以二四象限的角平分線為對稱軸的對稱線段CD,并直接寫出四邊形ABDC的面積為 ;
(2)若點C為格點(橫縱坐標均為整數),且AB⊥OC,且AB=OC,作出線段OC;并寫出C點坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形AEHC是由三個全等矩形拼成的,AH與BE、BF、DF、DG、CG分別交于點P、Q、K、M、N.設△BPQ,△DKM,△CNH的面積依次為S1,S2,S3.若S1+S3=20,則S2的值為( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)觀察與發現:小明將三角形紙片![]() 沿過點
沿過點![]() 的直線折疊,使得
的直線折疊,使得![]() 落在
落在![]() 邊上,折痕為
邊上,折痕為![]() ,展開紙片(如圖①);在第一次的折疊基礎上第二次折疊該三角形紙片,使點
,展開紙片(如圖①);在第一次的折疊基礎上第二次折疊該三角形紙片,使點![]() 和點
和點![]() 重合,折痕為
重合,折痕為![]() ,展平紙片后得到
,展平紙片后得到![]() (如圖②).小明認為
(如圖②).小明認為![]() 是等腰三角形,你同意嗎?請說明理由.
是等腰三角形,你同意嗎?請說明理由.
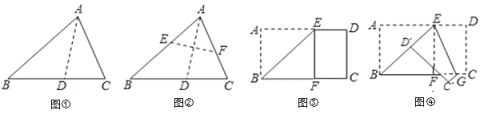
(2)實踐與運用:將矩形紙片![]() 沿過點
沿過點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,折痕為
處,折痕為![]() (如圖③);再沿過點
(如圖③);再沿過點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 上的點
上的點![]() 處,折痕為
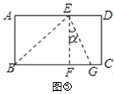
處,折痕為![]() (如圖④);再展平紙片(如圖⑤).求圖⑤中
(如圖④);再展平紙片(如圖⑤).求圖⑤中![]() 的大小。
的大小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com