
 如圖,二次函數y=x2-4x+3與坐標軸交于A、B、C三點,C點關于對稱軸的對稱點為D點,點P在拋物線上,且∠PDB=45°,求P點坐標.
如圖,二次函數y=x2-4x+3與坐標軸交于A、B、C三點,C點關于對稱軸的對稱點為D點,點P在拋物線上,且∠PDB=45°,求P點坐標. 分析 連結CD、BC,BC交PD于Q,作QH⊥x軸于H,如圖,通過解方程x2-4x+3=0得到A(1,0),B(3,0),則拋物線的對稱軸為直線x=2,再確定C(0,3)D(4,3),利用兩點間的距離公式計算出BD=$\sqrt{10}$,接著判定△OBC為等腰直角三角形得到BC=3$\sqrt{2}$,∠OCB=∠OBC=45°,然后證明△BDQ∽△BCD,利用相似比求出BQ=$\frac{5\sqrt{2}}{3}$,則在等腰直角三角形BHQ中,QH=BH=$\frac{\sqrt{2}}{2}$BQ=$\frac{5}{3}$,所以AH=OB-BH=$\frac{4}{3}$,于是得到Q($\frac{4}{3}$,$\frac{5}{3}$),接下來利用待定系數法求出直線DP的解析式為y=$\frac{1}{2}$x+1,最后通過解方程組$\left\{\begin{array}{l}{y={x}^{2}-4x+3}\\{y=\frac{1}{2}x+1}\end{array}\right.$得P點坐標.
解答 解:連結CD、BC,BC交PD于Q,作QH⊥x軸于H,如圖,
當y=0時,x2-4x+3=0,解得x1=1,x2=3,則A(1,0),B(3,0),
∴拋物線的對稱軸為直線x=2,
當x=0時,y=x2-4x+3=3,則C(0,3),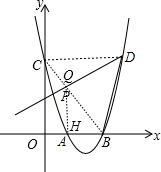
∵C點關于對稱軸的對稱點為D點,
∴D(4,3),
∴BD=$\sqrt{(4-3)^{2}+{3}^{2}}$=$\sqrt{10}$,
∵OB=OC=3,
∴△OBC為等腰直角三角形,
∴BC=3$\sqrt{2}$,∠OCB=∠OBC=45°,
∴∠BCD=45°,
∵∠PDB=45°,
∴∠BCD=∠BDQ,
而∠QBD=∠DBC,
∴△BDQ∽△BCD,
∴BQ:BD=BD:BC,即BQ:$\sqrt{10}$=$\sqrt{10}$:3$\sqrt{2}$,解得BQ=$\frac{5\sqrt{2}}{3}$,
在等腰直角三角形BHQ中,QH=BH=$\frac{\sqrt{2}}{2}$BQ=$\frac{5}{3}$,
∴AH=OB-BH=3-$\frac{5}{3}$=$\frac{4}{3}$,
∴Q($\frac{4}{3}$,$\frac{5}{3}$),
設直線DP的解析式為y=kx+b,
把D(4,3),Q($\frac{4}{3}$,$\frac{5}{3}$)代入得$\left\{\begin{array}{l}{4k+b=3}\\{\frac{4}{3}k+b=\frac{5}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直線DP的解析式為y=$\frac{1}{2}$x+1,
解方程組$\left\{\begin{array}{l}{y={x}^{2}-4x+3}\\{y=\frac{1}{2}x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{5}{4}}\end{array}\right.$,
∴P點坐標為($\frac{1}{2}$,$\frac{5}{4}$).
點評 本題考查了拋物線與x軸的交點:把求二次函數y=ax2+bx+c(a,b,c是常數,a≠0)與x軸的交點坐標問題轉化為解關于x的一元二次方程.也考查了相似三角形的判定與性質.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -0.01<x<0.02 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是一個棱長為10cm的正方體盒子,現需從底部A點處起,沿盒子的三個表面到頂部的B點處張貼一條彩色紙帶(紙帶的寬度忽略不計),則所需紙帶的最短長度是=10$\sqrt{10}$cm.
如圖是一個棱長為10cm的正方體盒子,現需從底部A點處起,沿盒子的三個表面到頂部的B點處張貼一條彩色紙帶(紙帶的寬度忽略不計),則所需紙帶的最短長度是=10$\sqrt{10}$cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在?ABCD中,AD=2AB,F是AD的中點,E是AB上一點,連接CF、EF,且CF=EF.
如圖,在?ABCD中,AD=2AB,F是AD的中點,E是AB上一點,連接CF、EF,且CF=EF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 為估計池塘兩岸A,B間的距離,楊陽在池塘一側選取了一點P,測得PA=16m,PB=12m,那么AB間的距離不可能是( )
為估計池塘兩岸A,B間的距離,楊陽在池塘一側選取了一點P,測得PA=16m,PB=12m,那么AB間的距離不可能是( )| A. | 15m | B. | 17m | C. | 20m | D. | 28m |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com