
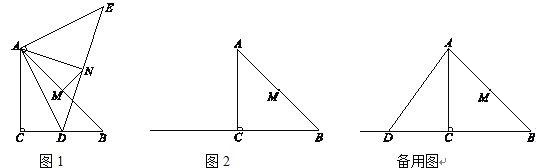
【題目】在△ABC中,∠ACB=90°,AC=BC=4,M為AB的中點.D是射線BC上一個動點,連接AD,將線段AD繞點A逆時針旋轉90°得到線段AE,連接ED,N為ED的中點,連接AN,MN.
(1)如圖1,當BD=2時,AN=___ __,NM與AB的位置關系是____ _____;
(2)當4<BD<8時,
①依題意補全圖2;
②判斷(1)中NM與AB的位置關系是否發生變化,并證明你的結論;
(3)連接ME,在點D運動的過程中,當BD的長為何值時,ME的長最小?最小值是多少?請直接寫出結果.
【答案】(1)![]() ,垂直;(2)①補圖見解析;②結論(1)成立,證明見解析.
,垂直;(2)①補圖見解析;②結論(1)成立,證明見解析.
【解析】試題分析:(1)由已知條件得到CD=2,由勾股定理求出AD,由旋轉的性質得到△ADE是等腰直角三角形,求出DE、AD的長度,再由直角三角形的性質推出AN=![]() DE,AM=
DE,AM=![]() AB,推出△ACD∽△AMN,根據三角形相似的性質即可得出結論;(2)①根據題意補全圖形即可;②根據等腰直角三角形性質得到∠CAB=∠B=45°,求得∠CAN +∠NAM=45°,根據旋轉的性質得到AD=AE,∠DAE=90°,推出△AMN∽△ADC,由三角形相似的性質得到∠AMN=∠ACD,即可得出結論;(3)連接ME、EB,過M 作MG⊥EB于點G,過A作AK⊥AB交BD于的延長線于K,得到△AKB是等腰直角三角形,推出△ADK≌△ABE,根據全等的性質可得∠ABE=∠K=45°,證得△BMG是等腰直角三角形,求出BC=4,AB=4
AB,推出△ACD∽△AMN,根據三角形相似的性質即可得出結論;(2)①根據題意補全圖形即可;②根據等腰直角三角形性質得到∠CAB=∠B=45°,求得∠CAN +∠NAM=45°,根據旋轉的性質得到AD=AE,∠DAE=90°,推出△AMN∽△ADC,由三角形相似的性質得到∠AMN=∠ACD,即可得出結論;(3)連接ME、EB,過M 作MG⊥EB于點G,過A作AK⊥AB交BD于的延長線于K,得到△AKB是等腰直角三角形,推出△ADK≌△ABE,根據全等的性質可得∠ABE=∠K=45°,證得△BMG是等腰直角三角形,求出BC=4,AB=4![]() ,MB=2
,MB=2![]() ,因為ME≥MG,所以當ME=MG時,ME的值最小,直接寫出結論即可.
,因為ME≥MG,所以當ME=MG時,ME的值最小,直接寫出結論即可.
試題解析:
(1)∵∠ACB=90°,AC=BC=4,BD=2,
∴AD=![]() =2
=2![]() ,
,
∵線段AD繞點A逆時針旋轉90°得到線段AE,
∴△ADE是等腰直角三角形,
∴DE=![]() AD=2
AD=2![]() ,
,
∵N是ED的中點,
∴AN=![]() DE=
DE=![]() ,
,
∵M是AB中點,
∴AM=![]() AB=2
AB=2![]() ,
,
∵![]() =
=![]() =
=![]() ,
, ![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠CAB=∠DAN=45°,
∴∠CAD=∠MAN,
∴△ACD∽△AMN,
∴∠AMN=∠C=90°,
∴MN⊥AB;
(2)①補全圖形如圖所示;
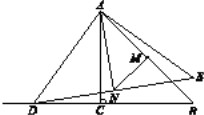
②結論:(1)中NM與AB的位置關系不變.
證明:∵∠ACB=90°,AC=BC,
∴∠CAB=∠B=45°,
∴∠CAN +∠NAM=45°,
∵AD繞點A逆時針旋轉90°得到線段AE,
∴AD=AE,∠DAE=90°,
∵N為ED的中點,
∴∠DAN=![]() ∠DAE=45°,AN⊥DE,
∠DAE=45°,AN⊥DE,
∴∠CAN +∠DAC =45°,∠AND=90°,
∴∠NAM =∠DAC,
在Rt△AND中, ![]() =cos∠DAN= cos45°=
=cos∠DAN= cos45°=![]() ,
,
在Rt△ACB中, ![]() =cos∠CAB= cos45°=
=cos∠CAB= cos45°=![]() ,
,
∵M為AB的中點,
∴AB=2AM,
∴![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∴△ANM∽△ADC ,
∴∠AMN=∠ACD,
∵點D在線段BC的延長線上,
∴∠ACD=180°-∠ACB =90°,
∴∠AMN=90°,
∴NM⊥AB.
(3)當BD的長為6時,ME的長的最小值為 2 .
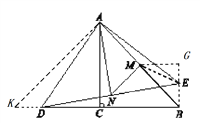
連接ME、EB,過M 作MG⊥EB于點G,過A作AK⊥AB交BD于的延長線于K,則△AKB是等腰直角三角形,
再△ADK和△ABE
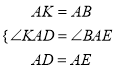 ,
,
∴△ADK≌△ABE,
∴∠ABE=∠K=45°,
∴△BMG是等腰直角三角形,
∵BC=4,
∴AB=4![]() ,MB=2
,MB=2![]() ,
,
∴MG=2,
∵∠G=90°,
∴ME≥MG,
∴當ME=MG時,ME的值最小,
∴ME=MG=2,
∴DK=BE=2,
∵CK=BC=4,
∴CD=2,
∴BD=6.
∴當BD的長為6時,ME的長的最小,最小值為 2 .


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】在以![]() 為原點的平面直角坐標系中,有不在坐標軸上的兩個點
為原點的平面直角坐標系中,有不在坐標軸上的兩個點![]() 、
、![]() ,設
,設![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標
的坐標![]()
(1)若![]() 與坐標軸平行,則
與坐標軸平行,則![]() ;
;
(2)若![]() 、
、![]() 、
、![]() 滿足
滿足![]() 和
和![]() ,
,![]() 軸,垂足為
軸,垂足為![]() ,
,![]() 軸,垂足為
軸,垂足為![]() .
.
①求四邊形![]() 的面積;
的面積;
②連![]() 、
、![]() 、
、![]() ,若
,若![]() 的面積大于
的面積大于![]() 而不大于
而不大于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在等邊三角形ABC中,BC=8cm,射線AG∥BC,點E從點A出發沿射線AG以1cm/s的速度運動,同時點F從點B出發沿射線BC以2cm/s的速度運動,設運動時間為t(s).
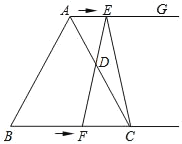
(1)連接EF,當EF經過AC邊的中點D時,求證:四邊形AFCE是平行四邊形;
(2)填空:①當t為 s時,四邊形ACFE是菱形;②當t為 s時,△ACE的面積是△ACF的面積的2倍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的頂點
的頂點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在反比例函數
在反比例函數![]() 的第一象限內的圖像上,
的第一象限內的圖像上,![]() ,
,![]() ,動點
,動點![]() 在
在![]() 軸的上方,且滿足
軸的上方,且滿足![]() .
.
(1)若點![]() 在這個反比例函數的圖像上,求點
在這個反比例函數的圖像上,求點![]() 的坐標;
的坐標;
(2)連接![]() 、
、![]() ,求
,求![]() 的最小值;
的最小值;
(3)若點![]() 是平面內一點,使得以
是平面內一點,使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形,則請你直接寫出滿足條件的所有點
為頂點的四邊形是菱形,則請你直接寫出滿足條件的所有點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將正方形 ABCD 繞點 A 按逆時針方向旋轉到正方形AB ' C ' D ' ,旋轉角為 ( 0<< 180 ) ,連接 B ' D 、 C ' D ,若 B ' D C ' D ,則 =____.

查看答案和解析>>
科目:初中數學 來源: 題型:
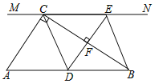
【題目】如圖,在![]() 中,
中,![]() ,過點
,過點![]() 的直線
的直線![]() ,
,![]() 為
為![]() 邊上一動點(不與
邊上一動點(不與![]() ,
,![]() 重合),過點
重合),過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,垂足為
,垂足為![]() ,連接
,連接![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)當![]() 移動到
移動到![]() 的什么位置時,四邊形
的什么位置時,四邊形![]() 是菱形?說明你的理由;
是菱形?說明你的理由;
(3)若點![]() 移動到
移動到![]() 中點,則當
中點,則當![]() 的大小滿足什么條件時,四邊形
的大小滿足什么條件時,四邊形![]() 是正方形?請說明你的理由.
是正方形?請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
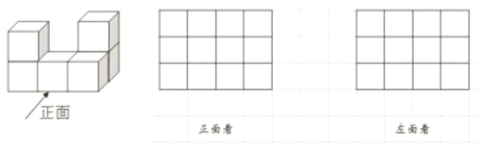
【題目】(1)按要求將下列幾何體進行分類,并將分類后幾何體的名稱寫在對應的括號內.

柱體:{ …}
錐體:{ …}
(2)6個完全相同的正方體組成如圖所示的幾何體,畫出該幾何體從正面,左面看到的形狀圖(用陰影畫在所給的方格中)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一只貓頭鷹蹲在一棵樹AC的B(點B在AC上)處,發現一只老鼠躲進短墻DF的另一側,貓頭鷹的視線被短墻遮住,為了尋找這只老鼠,它又飛至樹頂C處,已知短墻高DF=4米,短墻底部D與樹的底部A的距離為2.7米,貓頭鷹從C點觀測F點的俯角為53°,老鼠躲藏處M(點M在DE上)距D點3米.(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)貓頭鷹飛至C處后,能否看到這只老鼠?為什么?
(2)要捕捉到這只老鼠,貓頭鷹至少要飛多少米(精確到0.1米)?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),…,按這樣的運動規律,經過第2017次運動后,動點P的坐標是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com