
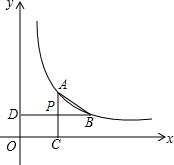
 如圖,已知點A、B在雙曲線y=$\frac{k}{x}$ (x>0)上,AC⊥x軸于C,BD⊥y軸于點D,AC與BD交于點P,P是AC的中點.
如圖,已知點A、B在雙曲線y=$\frac{k}{x}$ (x>0)上,AC⊥x軸于C,BD⊥y軸于點D,AC與BD交于點P,P是AC的中點.分析 (1)根據點P是AC的中點得到點A的橫坐標是m,結合反比例函數圖象上點的坐標特征來求點B的坐標;
(2)根據點P的坐標得到點P是BD的中點,所以由“對角線互相垂直平分的四邊形是菱形”得到四邊形ABCD是菱形;
(3)由△ABP的面積為3,知BP•AP=6.根據反比例函數 y=kx中k的幾何意義,知本題k=OC•AC,由反比例函數的性質,結合已知條件P是AC的中點,得出OC=BP,AC=2AP,進而求出k的值.
解答 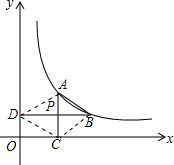 解:(1)∵A的橫坐標為m,AC⊥x軸于C,P是AC的中點,
解:(1)∵A的橫坐標為m,AC⊥x軸于C,P是AC的中點,
∴點B的橫坐標是2m.
又∵點B在雙曲線y=$\frac{k}{x}$ (x>0)上,
∴B(2m,$\frac{k}{2m}$).
(2)連接AD、CD、BC;
∵AC⊥x軸于C,BD⊥y軸于點D,
∴AC⊥BD;
∵A(m,$\frac{k}{m}$),B(2m,$\frac{k}{2m}$),
∴P(m,$\frac{k}{2m}$),
∴PD=PB,
又AP=PC,
∴四邊形ABCD是菱形;
(3)∵△ABP的面積為 $\frac{1}{2}$•BP•AP=3,
∴BP•AP=6,
∵P是AC的中點,
∴A點的縱坐標是B點縱坐標的2倍,
又∵點A、B都在雙曲線y=$\frac{k}{x}$(x>0)上,
∴B點的橫坐標是A點橫坐標的2倍,
∴OC=DP=BP,
∴k=OC•AC=BP•2AP=12.
∴該雙曲線的解析式是:y=$\frac{12}{x}$
點評 主要考查了反比例函數y=$\frac{k}{x}$中k的幾何意義,即過雙曲線上任意一點引x軸、y軸垂線,所得矩形面積為|k|,是經常考查的一個知識點;這里體現了數形結合的思想,做此類題一定要正確理解k的幾何意義.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
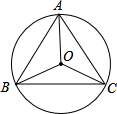 如圖是一個旋轉對稱圖形,以O為旋轉中心,以下列哪一個角為旋轉角旋轉,能使旋轉后的圖形與原圖形重合( )
如圖是一個旋轉對稱圖形,以O為旋轉中心,以下列哪一個角為旋轉角旋轉,能使旋轉后的圖形與原圖形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 售出件數 | 7 | 6 | 3 | 5 | 4 | 5 |
| 售價/元 | +3 | +2 | +1 | 0 | -1 | -1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com