
如圖,⊙O是△ABC的外接圓,AB為直徑,
=
,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求證:AE=CE;
(2)若AD=2,BD=8,求AF的長.
考點:圓周角定理,勾股定理,垂徑定理
專題:
分析:(1)如圖,作輔助線;證明
=,借助
=
,得到
=,即可解決問題.
(2)如圖,作輔助線;根據(jù)勾股定理求出CD;進而求出AE;證明△ADE∽△AFB,列出比例式即可解決問題.
解答: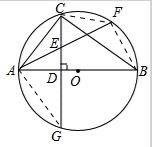
(1)證明:連接AG,CF.
∵AB為直徑,且AB⊥CG,
∴
=,
又∵
=
,
∴
=,
∴∠ACG=∠CAF,
∴AE=CE.
(2)連接BF;
∵AB為直徑,
∴∠ACB=90°,∠AFB=90°;而CD⊥AB,
∴CD
2=AD•BD=16,
∴CD=4;設(shè)AE=CE=λ,
∴DE=4-λ,由勾股定理得:
λ
2=2
2+(4-λ)
2,
解得:λ=2.5,即AE=2.5.
∵∠FAB=∠EAD,∠EDA=∠BFA,
∴△ADE∽△AFB,
∴AE:AB=AD:AF,而AB=10,AD=2,AE=2.5,
∴AF=8.
點評:本題主要考查了垂徑定理,圓周角定理.根據(jù)圓周角得出相關(guān)的角相等是本題的解題關(guān)鍵.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:初中數(shù)學(xué)
來源:
題型:
一件商品按成本價提高40%后標價,再打8折(標價的80%)銷售,售價為130元,設(shè)這件商品的成本價為x元,根據(jù)題意,下面所列方程正確的是( )
| A、40%×80%x=130 |
| B、40%x=130×80% |
| C、130×80%×40%=x |
| D、(1+40%)x×80%=130 |
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
某公司生產(chǎn)一種產(chǎn)品,每件成本價是400元,銷售價為510元,本季度銷售了5萬件,為進一步擴大市場,企業(yè)決定降低生產(chǎn)成本,經(jīng)過市場調(diào)研,預(yù)測下一季度這種商品每件銷售價會降低4%,銷售量將提高10%,要使銷售利潤(銷售利潤=銷售價-成本價)保持不變,該商品每件的成本應(yīng)降低多少元?
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
延長線段AB到C,使BC=
AB,D為AC的中點,DC=2,求AB的長.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
用計算器計算[12×(-4)-125÷(-5)]×(-2)
3=
.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
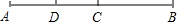
如圖,C,D是線段AB上兩點,若CB=5cm,DB=9cm,且D是AC的中點,則AC=
cm.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
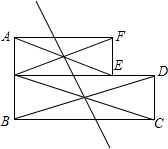
如圖是由兩個矩形組成的組合圖形,能否在圖形中找到一點P,沿過點P的某一條直線折疊該圖形,能將該圖形分成面積相等的兩部分?若能,請你在圖中做出點P,并說明點P的位置;若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:

如圖,在△ABC中,∠ACB=90°,AC=2,BC=
2,∠B=30°,F(xiàn)為AB的中點,AE平分∠BAC,點P為線段AE上一動點,則△BFP周長的最小值為
.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:
題型:
半徑為1和2的兩圓外切,與兩圓都內(nèi)切的圓的半徑r的取值范圍是
.
查看答案和解析>>

 如圖,⊙O是△ABC的外接圓,AB為直徑,
如圖,⊙O是△ABC的外接圓,AB為直徑,







 (1)證明:連接AG,CF.
(1)證明:連接AG,CF.







 如圖是由兩個矩形組成的組合圖形,能否在圖形中找到一點P,沿過點P的某一條直線折疊該圖形,能將該圖形分成面積相等的兩部分?若能,請你在圖中做出點P,并說明點P的位置;若不能,請說明理由.
如圖是由兩個矩形組成的組合圖形,能否在圖形中找到一點P,沿過點P的某一條直線折疊該圖形,能將該圖形分成面積相等的兩部分?若能,請你在圖中做出點P,并說明點P的位置;若不能,請說明理由. 如圖,在△ABC中,∠ACB=90°,AC=2,BC=2
如圖,在△ABC中,∠ACB=90°,AC=2,BC=2