Question

9．已知在平面直角坐標系中，拋物線y=-$\frac{1}{2}{x^2}$+bx+c與x軸相交于點A，B，與y軸相交于點C，直線y=x+4經過A，C兩點，
（1）求拋物線的表達式；
（2）如果點P，Q在拋物線上（P點在對稱軸左邊），且PQ∥AO，PQ=2AO，求P，Q的坐標；
（3）動點M在直線y=x+4上，且△ABC與△COM相似，求點M的坐標．

Answer 1

分析 （1）根據自變量與函數值的對應關系，可得A、C點坐標，根據待定系數法，可得函數解析式；
（2）根據平行于x軸的直線與拋物線的交點關于對稱軸對稱，可得P、Q關于直線x=-1對稱，根據PQ的長，可得P點的橫坐標，Q點的橫坐標，根據自變量與函數值的對應關系，可得答案；
（3）根據兩組對邊對應成比例且夾角相等的兩個三角形相似，可得CM的長，根據等腰直角三角形的性質，可得MH的長，再根據自變量與函數值的對應關系，可得答案．

解答 解：（1）當x=0時，y=4，即C（0，4），
當y=0時，x+4=0，解得x=-4，即A（-4，0），
將A、C點坐標代入函數解析式，得
$\left\{\begin{array}{l}{-\frac{1}{2}×（-4）^{2}-4b+4=0}\\{c=4}\end{array}\right.$，
解得$\left\{\begin{array}{l}{b=-1}\\{c=4}\end{array}\right.$，
拋物線的表達式為y=-$\frac{1}{2}{x^2}$-x+4；
（2）PQ=2AO=8，
又PQ∥AO，即P、Q關于對稱軸x=-1對稱，
PQ=8，-1-4=-5，
當x=-5時，y=-$\frac{1}{2}$×（-5）²-（-5）+4=-$\frac{7}{2}$，即P（-5，-$\frac{7}{2}$）；
-1+4=3，即Q（3，-$\frac{7}{2}$）；
P點坐標（-5，-$\frac{7}{2}$），Q點坐標（3，-$\frac{7}{2}$）；
（3）∠MCO=∠CAB=45°，
①當△MCO∽△CAB時，$\frac{OC}{BA}$=$\frac{CM}{AC}$，即$\frac{4}{6}$=$\frac{CM}{4\sqrt{2}}$，
CM=$\frac{8\sqrt{2}}{3}$．
如圖1，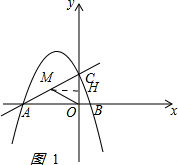
過M作MH⊥y軸于H，MH=CH=$\frac{\sqrt{2}}{2}$CM=$\frac{8}{3}$，
當x=-$\frac{8}{3}$時，y=-$\frac{8}{3}$+4=$\frac{4}{3}$，
∴M（-$\frac{8}{3}$，$\frac{4}{3}$）；
當△OCM∽△CAB時，$\frac{OC}{CA}$=$\frac{CM}{AB}$，即$\frac{4}{4\sqrt{2}}$=$\frac{CM}{6}$，解得CM=3$\sqrt{2}$，
如圖2，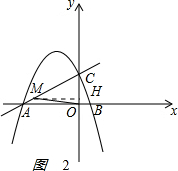
過M作MH⊥y軸于H，MH=CH=$\frac{\sqrt{2}}{2}$CM=3，
當x=-3時，y=-3+4=1，
∴M（-3，1），
綜上所述：M點的坐標為（-$\frac{8}{3}$，$\frac{4}{3}$），（-3，1）．

點評 本題考查了二次函數綜合題，利用待定系數法求函數解析式；利用平行于x軸的直線與拋物線的交點關于對稱軸對稱得出P、Q關于直線x=-1對稱是解題關鍵；利用兩組對邊對應成比例且夾角相等的兩個三角形得出CM的長是解題關鍵．