
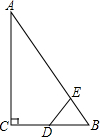
 如圖,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D為BC的中點,若動點E以1cm/s的速度從A點出發,沿著A→B的方向運動,設E點的運動時間為t秒,連接DE,當△BDE是直角三角形時,t的值為2或3.5.
如圖,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D為BC的中點,若動點E以1cm/s的速度從A點出發,沿著A→B的方向運動,設E點的運動時間為t秒,連接DE,當△BDE是直角三角形時,t的值為2或3.5. 分析 先求出AB的長,再分①∠BDE=90°時,DE是△ABC的中位線,然后求出AE的長度,再分點E在AB上和在BA上兩種情況列出方程求解即可;②∠BED=90°時,利用∠B的余弦列式求出BE,然后分點E在AB上和在BA上兩種情況列出方程求解即可.
解答 解:∵∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=BC÷cos60°=2÷$\frac{1}{2}$=4,
①∠BDE=90°時,
∵D為BC的中點,
∴DE是△ABC的中位線,
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2(cm),
點E在AB上時,t=2÷1=2(秒),
點E在BA上時,點E運動的路程為4×2-2=6(cm),
∴t=6÷1=6(秒)(舍去);
②∠BED=90°時,BE=BD•cos60°=$\frac{1}{2}$×2×$\frac{1}{2}$=0.5,
點E在AB上時,t=(4-0.5)÷1=3.5(秒),
綜上所述,t的值為2或3.5,
故答案為:2或3.5
點評 本題考查了相似三角形的問題,關鍵是根據三角形的中位線定理,解直角三角形的相關知識,難點在于分情況討論.


科目:初中數學 來源: 題型:選擇題
| A. | y1>0,y2>0 | B. | y1>0,y2<0 | C. | y1<0,y2>0 | D. | y1<0,y2<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | 0 | 3 |
| y | 2 | 0 |
| A. | k=2,b=3 | B. | k=-$\frac{2}{3}$,b=2 | C. | k=3,b=2 | D. | k=1,b=-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1:3 | B. | 3:9 | C. | 8:1 | D. | 8:9 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 24cm2 | B. | 12cm2 | C. | 6cm2 | D. | 3cm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com