
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() 為坐標原點.拋物線
為坐標原點.拋物線![]() 分別交
分別交![]() 軸于
軸于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,
,![]() .
.
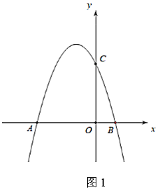
(1)求該拋物線的解析式.
(2)如圖2,點![]() 為第二象限拋物線上一點,過點
為第二象限拋物線上一點,過點![]() 作
作![]() 于點
于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,線段
,線段![]() 的長度為
的長度為![]() ,求
,求![]() 與
與![]() 的函數關系式(不要求寫出自變量
的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
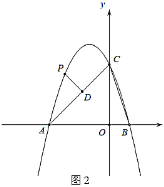
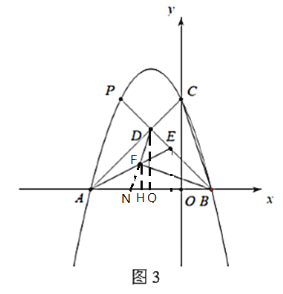
(3)在(2)的條件下,當直線![]() 經過點
經過點![]() 時,如圖3,點
時,如圖3,點![]() 在線段
在線段![]() 上,點
上,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的長.
的長.
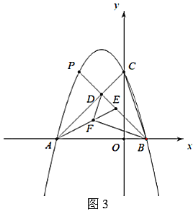
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用OA=OC,待定系數法求解二次函數解析式.
(2)過P作![]() 軸的垂線,用銳角三角函數建立PD與PM之間的聯系,用二次函數與一次函數求解PM的長度,從而得到答案.
軸的垂線,用銳角三角函數建立PD與PM之間的聯系,用二次函數與一次函數求解PM的長度,從而得到答案.
(3)延長DF交AB于N,過F,D作好AB的垂線,利用面積與相似三角形求解FN,,DN的數量關系,再利用![]() ,找到
,找到![]() ,利用相似三角形性質表示AN的長,最后化歸到直角三角形DNQ中,利用勾股定理得到答案.
,利用相似三角形性質表示AN的長,最后化歸到直角三角形DNQ中,利用勾股定理得到答案.
解:(1)因為:![]() ,
,
所以點C![]() ,所以
,所以![]() ,
,
又因為![]()
所以![]() ,把
,把![]() 代入解析式得:
代入解析式得:
![]() ,即
,即![]()
解得:![]() (舍去),所以
(舍去),所以![]() ,
,
所以拋物線為![]()
(2)如圖,過P作![]() 軸與N,交AC于M,又
軸與N,交AC于M,又![]() ,
,![]()
所以![]() .
.
因為![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]()
所以![]()
由(1)得![]() ,所以 直線AC為
,所以 直線AC為![]() ,
,
因為![]() ,
,![]() 軸,
軸,
所以![]()
所以![]()
所以![]()
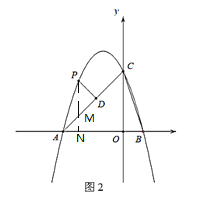
(3)如圖,延長DF交AB于N,過F,D分別作![]() ,垂足分別為H,Q,因為拋物線為
,垂足分別為H,Q,因為拋物線為![]() ,所以B(1,0),A(-3,0)
,所以B(1,0),A(-3,0)
所以AB=4,因為![]() 的面積為
的面積為![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因為A(-3,0),C(0,-3),![]()
所以![]()
因為![]()
所以![]()
所以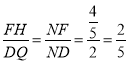
設![]() ,則
,則![]()
因為![]() ,
,![]() ,
,
所以![]()
所以![]() ,
,
又因為![]()
所以![]()
所以![]() 所以
所以![]() ,
,
所以![]()
在直角三角形DNQ中,![]()
所以![]()
解得:![]() ,(負根舍去)
,(負根舍去)
所以![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
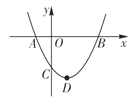
【題目】如圖,二次函數![]() (
(![]() )圖象的頂點為
)圖象的頂點為![]() ,其圖象與
,其圖象與![]() 軸的交點
軸的交點![]() ,
,![]() 的橫坐標分別為
的橫坐標分別為![]() 和3.下列結論:
和3.下列結論:
①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時,![]() 是等腰直角三角形.其中結論正確的個數是( )
是等腰直角三角形.其中結論正確的個數是( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線![]() 與
與![]() 軸交于點
軸交于點![]() ,且過拋物線
,且過拋物線![]() 的頂點
的頂點![]() 和拋物線上的另一點
和拋物線上的另一點![]() .
.
(1)若點![]()
①求拋物線解析式;
②若![]() ,求直線解析式.
,求直線解析式.
(2)若![]() ,過點
,過點![]() 作
作![]() 軸的平行線與拋物線的對稱軸交于點
軸的平行線與拋物線的對稱軸交于點![]() ,當
,當![]() 時,求
時,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
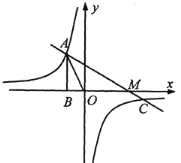
【題目】如圖,已知反比例函數 y=![]() 的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為
的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為![]() .
.
(1)求a、k的值;
(2)若一次函數y=mx+n圖像經過點A和反比例函數圖像上另一點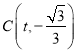 ,且與x軸交于M點,求AM的值:
,且與x軸交于M點,求AM的值:
(3)在(2)的條件下,如果以線段AM為一邊作等邊△AMN,頂點N在一次數函數y=bx上,則b= ______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級有1200名學生,在體育考試前隨機抽取部分學生進行跳繩測試,根據測試成績制作了下面兩個統計圖.請根據相關信息,解答下列問題:

(Ⅰ)本次參加跳繩測試的學生人數為___________,圖①中![]() 的值為___________;
的值為___________;
(Ⅱ)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(Ⅲ)根據樣本數據,估計該校九年級跳繩測試中得3分的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果店計劃進A,B兩種水果共140千克,這兩種水果的進價和售價如表所示
進價 | 售價 | |
A種水果 | 5 | 8 |
B種水果 | 9 | 13 |
![]() 若該水果店購進這兩種水果共花費1020元,求該水果店分別購進A,B兩種水果各多少千克?
若該水果店購進這兩種水果共花費1020元,求該水果店分別購進A,B兩種水果各多少千克?
![]() 在
在![]() 的基礎上,為了迎接春節的來臨,水果店老板決定把A種水果全部八折出售,B種水果全部降價
的基礎上,為了迎接春節的來臨,水果店老板決定把A種水果全部八折出售,B種水果全部降價![]() 出售,那么售完后共獲利多少元?
出售,那么售完后共獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】位于重慶市匯北區的照母山森林公園乘承“近自然”生態理念營造森林風景,“雖由人作,宛自天開”,凸顯自然風骨與原生野趣.山中最為矚目的經典當屬攬星塔.登臨塔頂,可上九天邀月攬星,可鳥瞰新區,領略附近樓宇的壯美;亦可遠眺兩江勝景.登臨此塔,讓你有飄然若仙的聯想又有登高遠眺,“一覽眾山小”的震撼,我校某數學興趣小組的同學準備利用所學的三角函數知識估測該塔的高度,已知攬星塔AB位于坡度l=![]() :1的斜坡BC上,測量員從斜坡底端C處往前沿水平方向走了120m達到地面D處,此時測得攬星塔AB頂端A的仰角為37°,攬星塔底端B的仰角為30°,已知A、B、C、D在同一平面內,則該塔AB的高度為( )m,(結果保留整數,參考數據;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
:1的斜坡BC上,測量員從斜坡底端C處往前沿水平方向走了120m達到地面D處,此時測得攬星塔AB頂端A的仰角為37°,攬星塔底端B的仰角為30°,已知A、B、C、D在同一平面內,則該塔AB的高度為( )m,(結果保留整數,參考數據;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
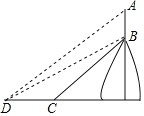
A.31B.40C.60D.136
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
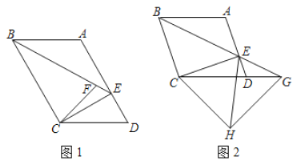
(1)如圖1,點![]() 是
是![]() 上一點,連接
上一點,連接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,若![]() ,延長
,延長![]() 交
交![]() 延長線于點
延長線于點![]() ,以
,以![]() 為斜邊做等腰直角
為斜邊做等腰直角![]() ,連接
,連接![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com