
【題目】如圖,在數軸上A點表示數a,B點表示數b,AB表示A點和B點之間的距離,且a、b滿足![]() .
.
(1)求A,B兩點之間的距離;
(2)若在數軸上存在一點C,且AC=2BC,求C點表示的數;
(3)若在原點O處放一擋板,一小球甲從點A處以1個單位/秒的速度向左運動;同時另一小球乙從點B處以2個單位/秒的速度也向左運動,在碰到擋板后(忽略球的大小,可看作一點)以原來的速度向相反的方向運動,設運動的時間為t(秒).
①分別表示甲、乙兩小球到原點的距離(用t表示);
②求甲、乙兩小球到原點的距離相等時經歷的時間.
![]()
【答案】(1)8;(2)c=![]() 或c=14;(3)t=
或c=14;(3)t=![]() 秒或t=8秒.
秒或t=8秒.
【解析】試題分析:(1)先根據非負數的性質求出a、b的值,再根據兩點間的距離公式即可求得A、B兩點之間的距離;(2)分C點在線段AB上和線段AB的延長線上兩種情況討論即可求解;(3)①甲球到原點的距離=甲球運動的路程+OA的長,乙球到原點的距離分兩種情況:(Ⅰ)當0<t≤3時,乙球從點B處開始向左運動,一直到原點O,此時OB的長度-乙球運動的路程即為乙球到原點的距離;(Ⅱ)當t>3時,乙球從原點O處開始向右運動,此時乙球運動的路程-OB的長度即為乙球到原點的距離;②分兩種情況:(Ⅰ)0<t≤3,(Ⅱ)t>3,根據甲、乙兩小球到原點的距離相等列出關于t的方程,解方程即可.
試題解析:
(1)∵![]() ,∴a+2=0,b+3a=0,∴a=2,b=6;
,∴a+2=0,b+3a=0,∴a=2,b=6;
∴AB的距離=|ba|=8;
(2)設數軸上點C表示的數為c.
∵AC=2BC,∴|ca|=2|cb|,即|c+2|=2|c6|.
∵AC=2BC>BC,∴點C不可能在BA的延長線上,則C點可能在線段AB上和線段AB的延長線上.
①當C點在線段AB上時,則有2≤c≤6,得c+2=2(6c),解得c=![]() ;
;
②當C點在線段AB的延長線上時,則有c>6,得c+2=2(c6),解得c=14.
故當AC=2BC時,c=![]() 或c=14;
或c=14;
(3)①∵甲球運動的路程為:1t=t,OA=2,∴甲球與原點的距離為:t+2;
乙球到原點的距離分兩種情況:
(Ⅰ)當0<t≤3時,乙球從點B處開始向左運動,一直到原點O,∵OB=6,乙球運動的路程為:2t=2t,∴乙球到原點的距離為:62t;
(Ⅱ)當t>3時,乙球從原點O處開始一直向右運動,此時乙球到原點的距離為:2t6;
②當0<t≤3時,得t+2=62t,解得t=![]() ;
;
當t>3時,得t+2=2t6,解得t=8.
故當t=![]() 秒或t=8秒時,甲乙兩小球到原點的距離相等.
秒或t=8秒時,甲乙兩小球到原點的距離相等.


科目:初中數學 來源: 題型:
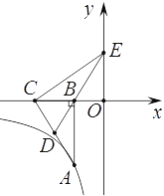
【題目】如圖,已知點A在反比例函數![]() 上,作Rt△ABC,點D為斜邊AC的中點,連DB并延長交y軸于點E,若△BCE的面積為8。
上,作Rt△ABC,點D為斜邊AC的中點,連DB并延長交y軸于點E,若△BCE的面積為8。
(1)求證:△EOB∽△ABC;
(2)求反比例函數的解析式。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解九年級學生的體能情況,抽調了一部分學生進行一分鐘跳繩測試,將測試成績整理后作出如下統計圖.甲同學計算出第二組的頻率是0.08,乙同學計算出從左至右第一、二、三、四組的頻數比為2:4:17:15.結合統計圖回答下列問題:
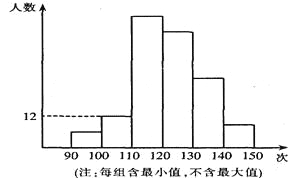
(1)這次共抽調了多少人?
(2)若跳繩次數不少于130次為優秀,則這次測試成績的優秀率是多少?
(3)若該校九年級有600名學生,請估計該校九年級達到優秀的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,求1+2-1+2-2+…+2-2 016的值.
解:設S=1+2-1+2-2+…+2-2016, ①
則2S=2+1+2-1+…+2-2 015, ②
②-①得S=2-2-2 016.
請你仿此計算:
(1)1+3-1+3-2+…+3-2 016;
(2)1+3-1+3-2+…+3-n(n為正整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,O,B在同一條直線上,∠AOD=∠BOD=∠EOC=90°,∠BOC∶∠AOE=3∶1.
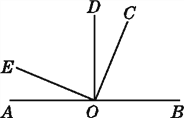
(1)求∠COD的度數.
(2)圖中有哪幾對角互為余角?
(3)圖中有哪幾對角互為補角?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據某地實驗測得的數據表明,高度每增加1km,氣溫大約下降3℃,已知該地地面溫度為21℃.
(1)高空某處高度是6km,求此處的溫度是多少;
(2)高空某處溫度為﹣24℃,求此處的高度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com