
分析 先由2x-3y=0得到y=$\frac{2}{3}$x=$\frac{2}{3}a$,與x=a一起代入(k-1)x+(k+1)y=4,求得a,再根據a<0,得到關于k的不等式,解不等式可求k的取值范圍.
解答 解:由2x-3y=0得y=$\frac{2}{3}$x=$\frac{2}{3}a$,
與x=a一起代入(k-1)x+(k+1)y=4,
(k-1)a+(k+1)×$\frac{2}{3}a$=4,
解得a=$\frac{12}{5k-1}$,
∵a<0,
∴$\frac{12}{5k-1}$<0,
解得k<$\frac{1}{5}$.
故k的取值范圍是k<$\frac{1}{5}$.
故答案為:k<$\frac{1}{5}$.
點評 本題考查了解二元一次方程,解一元一次不等式組,解題的關鍵是把k看做已知數得到關于k的不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 3m2n與-4nm2 | B. | $\frac{1}{3}$xy2與$\frac{1}{3}$x2y2 | C. | -5ab與2×103ab | D. | 35與-12 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將△ABC繞點C順時針旋轉90°后得到△A′B′C′,則點A的對應點A′的坐標為( )
如圖,將△ABC繞點C順時針旋轉90°后得到△A′B′C′,則點A的對應點A′的坐標為( )| A. | (0,$\sqrt{2}$) | B. | (0,-3) | C. | (-1,0) | D. | (3,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
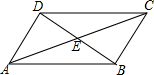 如圖,在四邊形ABCD中,對角線AC、BD相交于點E,∠CBD=90°,BC=4,BE=ED=3,AC=10,則四邊形ABCD的面積為24.
如圖,在四邊形ABCD中,對角線AC、BD相交于點E,∠CBD=90°,BC=4,BE=ED=3,AC=10,則四邊形ABCD的面積為24.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com