
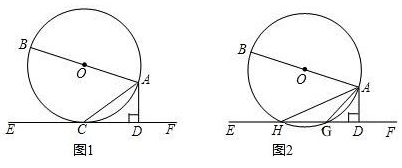
分析 (1)連接OC.只要證明∠ACD+∠OAC=90°,∠CAD+∠ACD=90°即可解決問題.
(2)如圖2中,連接BH.首先證明∠AGD=∠B,由∠B+∠BAH=90°,∠GAD+∠AGD=90°,即可證明.
(3)在Rt△ABH中,首先求出AH、BH,由HA平分∠BAG,推出$\widehat{BH}$=$\widehat{GH}$,推出BH=HG=2,由△ABH∽△AGD,
推出$\frac{AD}{DG}$=$\frac{AH}{BH}$=$\frac{4}{2}$=2,推出AD=2DG,設DG=x,則AD=2x,在Rt△AHD中,根據AH2=AD2+DH2,可得42=(2x)2+(2+x)2,解方程即可.
解答 (1)證明:如圖1中,連接OC.
∵EF是⊙O的切線,
∴OC⊥EF,
∴∠OCA+∠ACD=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠ACD+∠OAC=90°,
∵AD⊥CD,
∴∠ADC=90°,
∴∠CAD+∠ACD=90°,
∴∠BAC=CAD.
(2)證明:如圖2中,連接BH.
∵∠B+∠AGH=180°,∠AGH+∠AGD=180°,
∴∠AGD=∠B,
∵AB是直徑,
∴∠AHB=90°,
∴∠B+∠BAH=90°,
∵∠GAD+∠AGD=90°,
∴∠BAH=∠GAD.
(3)解:在圖2中,在Rt△ABH中,AB=2$\sqrt{5}$,cos∠BAH=$\frac{2\sqrt{5}}{5}$,
AH=AB•cosBAH=2$\sqrt{5}$•$\frac{2\sqrt{5}}{5}$=4,BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=2,
∵HA平分∠BAG,
∴$\widehat{BH}$=$\widehat{GH}$,
∴BH=HG=2,
∵∠BHA=∠GAD,∠AHB=∠ADG=90°,
∴△ABH∽△AGD,
∴$\frac{AD}{DG}$=$\frac{AH}{BH}$=$\frac{4}{2}$=2,
∴AD=2DG,設DG=x,則AD=2x,
在Rt△AHD中,
∵AH2=AD2+DH2,
∴42=(2x)2+(2+x)2,
解得x=$\frac{6}{5}$或2(舍棄),
∴DG=$\frac{6}{5}$.
點評 本題考查圓綜合題、切線的性質、相似三角形的判定和性質、勾股定理、銳角三角函數等知識,解題的關鍵是學會添加常用輔助線,學會構建方程解決問題,屬于中考壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
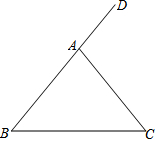 如圖,在△ABC中,AB=AC,∠DAC是△ABC的一個外角.
如圖,在△ABC中,AB=AC,∠DAC是△ABC的一個外角.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
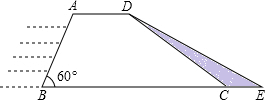 水利部門決定對某水庫大壩進行加固,大壩的橫截面是梯形ABCD.如圖所示,已知迎水坡面AB的長為4米,∠B=60°,背水坡面CD的長為4$\sqrt{3}$米,加固后大壩的橫截面積為梯形ABED,CE的長為2米.
水利部門決定對某水庫大壩進行加固,大壩的橫截面是梯形ABCD.如圖所示,已知迎水坡面AB的長為4米,∠B=60°,背水坡面CD的長為4$\sqrt{3}$米,加固后大壩的橫截面積為梯形ABED,CE的長為2米.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com