
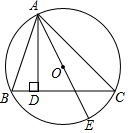
 如圖,AD為△ABC的高,AE為△ABC外接圓的直徑,且AD=$\frac{1}{2}$AE=2$\sqrt{3}$,AB:AC=2:3,求sinB的值.
如圖,AD為△ABC的高,AE為△ABC外接圓的直徑,且AD=$\frac{1}{2}$AE=2$\sqrt{3}$,AB:AC=2:3,求sinB的值. 分析 連接CE,根據圓周角定理得到∠ACE=90°,設AB=2k,AC=3k,根據相似三角形的性質得到k=2,求得AB=4,然后根據三角函數的定義即可得到結論.
解答  解:連接CE,
解:連接CE,
∴∠B=∠E,
∵AE為△ABC外接圓的直徑,
∴∠ACE=90°,
∵AD=$\frac{1}{2}$AE=2$\sqrt{3}$,
∴AE=4$\sqrt{3}$,
∵AB:AC=2:3,
∴設AB=2k,AC=3k,
∵AD為△ABC的高,
∴∠ADB=∠ACE=90°,
∴△ABD∽△AEC,
∴$\frac{AB}{AE}$=$\frac{AD}{AC}$,
∴$\frac{2k}{4\sqrt{3}}=\frac{2\sqrt{3}}{3k}$,
∴k=2,
∴AB=4,
∴sinB=$\frac{AD}{AB}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$.
點評 此題考查了相似三角形的判定和性質,圓周角定理與三角函數的定義.此題難度不大,注意掌握輔助線的作法,注意掌握數形結合思想與轉化思想的應用.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
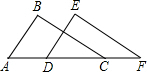 如圖,已知點A、D、C、F在同一直線上,且AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加的一個條件是( )
如圖,已知點A、D、C、F在同一直線上,且AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加的一個條件是( )| A. | ∠B=∠E | B. | ∠A=∠EDF | C. | ∠BCA=∠F | D. | BC∥EF |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
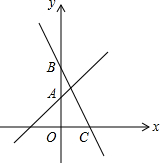 如圖,已知函數y=x+2的圖象與y軸交于點A,一次函數y=kx+b的圖象經過點B(0,4)且與x軸及y=x+2的圖象分別交于點C、D,點D的坐標為($\frac{2}{3}$,n).
如圖,已知函數y=x+2的圖象與y軸交于點A,一次函數y=kx+b的圖象經過點B(0,4)且與x軸及y=x+2的圖象分別交于點C、D,點D的坐標為($\frac{2}{3}$,n).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com