Question

2．已知△ABC內接于⊙O，請僅用無刻度的直尺，根據下列條件分別在圖1，圖2中畫出∠BAC的平分線（保留作圖痕跡，不寫作法）．

（1）如圖1，P是BC邊的中點；
（2）如圖2，直線l與⊙O相切于點P，且l∥BC．

Answer 1

分析 （1）連接OP并延長，交⊙O于D，根據P是BC邊的中點，可得OD垂直平分BC，進而得到點D為$\widehat{BC}$的中點，連接AD，則∠BAD=∠CAD，因此AD即為所求；
（2）連接PO并延長，交⊙O于E，根據直線l與⊙O相切于點P，且l∥BC，可得PE垂直平分BC，進而得到點E為$\widehat{BC}$的中點，連接AE，則∠BAE=∠CAE，因此AE即為所求．

解答 解：（1）如圖所示，AD 即為所求；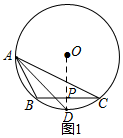


（2）如圖所示，AE即為所求．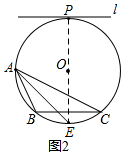

點評 本題主要考查了復雜作圖、圓周角定理、垂徑定理以及切線的性質的綜合應用，解決問題的關鍵是掌握：平分弦（不是直徑）的直徑垂直于弦，并且平分弦所對的兩條弧．解題時注意：在同圓或等圓中，同弧或等弧所對的圓周角相等．