
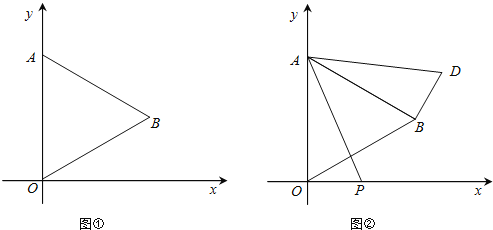
【題目】在平面直角坐標系中,已知點O為坐標原點,點A(0,4).△AOB是等邊三角形,點B在第一象限.
(1)如圖①,求點B的坐標;
(2)點P是x軸上的一個動點,連接AP,以點A為旋轉中心,把△AOP逆時針旋轉,使邊AO與AB重合,得△ABD.
①如圖②,當點P運動到點(![]() ,0)時,求此時點D的坐標;
,0)時,求此時點D的坐標;
②求在點P運動過程中,使△OPD的面積等于![]() 的點P的坐標(直接寫出結果即可).
的點P的坐標(直接寫出結果即可).
【答案】(1)(![]() ,2);(2)①點D坐標(
,2);(2)①點D坐標(![]() ,
,![]() ),②點P的坐標分別為(
),②點P的坐標分別為(![]() ,0)、(
,0)、(![]() ,0)、(
,0)、(![]() ,0)、(
,0)、(![]() ,0).
,0).
【解析】
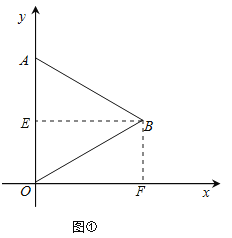
(1)過點B作BE⊥y軸于點E,作BF⊥x軸于點F.依題意得BF=OE=2,利用勾股定理求出OF,然后可得點B的坐標.
(2)①由△ABD由△AOP旋轉得到,證明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等邊三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函數求出BG=BDcos60°,DG=BDsin60°.然后求出OH,DH,然后求出點D的坐標.
②本題分三種情況進行討論,設點P的坐標為(x,0):第一種情況:當點P在x軸正半軸上時,第二種情況:當P在x軸負半軸,OP<![]() 時,第三種情況:當點P在x軸的負半軸上,且OP≥
時,第三種情況:當點P在x軸的負半軸上,且OP≥![]() 時,此時點D在x軸上或第四象限.綜合上面三種情況即可求出符合條件的值.
時,此時點D在x軸上或第四象限.綜合上面三種情況即可求出符合條件的值.
解:(1)如圖①,過點B作BE⊥y軸于點E,作BF⊥x軸于點F,
∵△AOB是等邊三角形,OA=4,
∴BF=OE=2.
在Rt△OBF中,
由勾股定理,得:![]() ,
,
∴點B的坐標為(![]() ,2).
,2).
(2)①如圖②,過點B作BE⊥y軸于點E,作BF⊥x軸于點F,過點D作DH⊥x軸于點H,延長EB交DH于點G.則BG⊥DH.
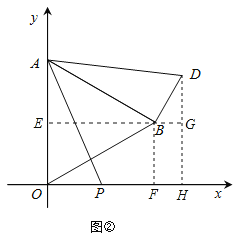
∵△ABD由△AOP旋轉得到,
∴△ABD≌△AOP.
∴∠ABD=∠AOP=90°,![]() .
.
∵△AOB是等邊三角形,
∴∠ABO=60°.
∵BE⊥OA,
∴∠ABE=30°,
∴∠DBG=60°
在Rt△DBG中,![]() .
.
∵sin60°=![]() ,
,
∴DG=DBsin60°=![]() ,
,
∴![]() ,
,![]() .
.
∴點D的坐標為(![]() ,
,![]() ).
).
②點P的坐標分別為:(![]() ,0)、(
,0)、(![]() ,0)、(
,0)、(![]() ,0)、(
,0)、(![]() ,0).
,0).
假設存在點P,在它運動過程中,使△OPD的面積等于![]() .
.
設OP=x,下面分三種情況討論.
第一種情況:
當點P在x軸正半軸上時,如圖③,BD=OP=x,
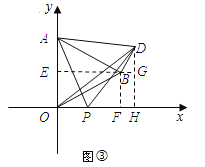
在Rt△DBG中,∠DBG=60°,
∴DG=BDsin60°=![]() ,
,
∴![]() .
.
∵△OPD的面積等于![]() ,
,
∴![]() ,
,![]() .
.
解得:![]() ,
,![]() (舍去).
(舍去).
∴點P1的坐標為(![]() ,0).
,0).
第二種情況:
當點P在x軸的負半軸上,且OP<![]() 時,此時點D在第一象限,如圖④,
時,此時點D在第一象限,如圖④,

在Rt△DBG中,∠DBG=30°,BG=BDcos30°=![]() .
.
∴![]() ,
,
∵△OPD的面積等于![]() ,
,
∴![]() ,
,![]() .
.
解得:![]() ,
,![]() .
.
∴點P2的坐標為(![]() ,0).點P3的坐標為(
,0).點P3的坐標為(![]() ,0).
,0).
第三種情況:
當點P在x軸的負半軸上,且OP≥![]() 時,此時點D在x軸上或第四象限,如圖⑤,
時,此時點D在x軸上或第四象限,如圖⑤,
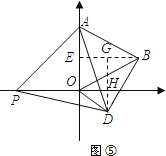
在Rt△DBG中,∠DBG=60°,
∴DG=BDsin60°=![]() .
.
∵△OPD的面積等于![]() ,
,
∴![]() ,
,![]() .
.
解得:![]() ,
,![]() (舍去).
(舍去).
∴點P4的坐標為:(![]() ,0).
,0).
綜上所述,點P的坐標為:P1(![]() ,0)或P2(
,0)或P2(![]() ,0)或P3(
,0)或P3(![]() ,0)或P4(
,0)或P4(![]() ,span>0).
,span>0).


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】取一副三角板按如圖所示拼接,固定三角板ADC,將三角板ABC繞點A順時針方向旋轉,旋轉角度為α(0°<α≤45°),得到△ABC′.

①當α為多少度時,AB∥DC?
②當旋轉到圖③所示位置時,α為多少度?
③連接BD,當0°<α≤45°時,探求∠DBC′+∠CAC′+∠BDC值的大小變化情況,并給出你的證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面關于x的方程中:①ax2+x+2=0;②3(x﹣9)2﹣(x+1)2=1;③x+3=![]() ;④(a2+a+1)x2﹣a=0;⑤
;④(a2+a+1)x2﹣a=0;⑤![]() =x﹣1.一元二次方程的個數是( )
=x﹣1.一元二次方程的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,一次函數y=﹣![]() x+3的圖象與x軸交于點A,與y軸交于B點,拋物線y=﹣x2+bx+c經過A,B兩點,在第一象限的拋物線上取一點D,過點D作DC⊥x軸于點C,交直線AB于點E.
x+3的圖象與x軸交于點A,與y軸交于B點,拋物線y=﹣x2+bx+c經過A,B兩點,在第一象限的拋物線上取一點D,過點D作DC⊥x軸于點C,交直線AB于點E.
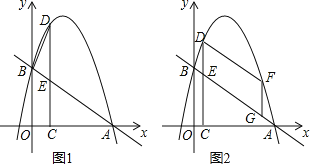
(1)求拋物線的函數表達式
(2)是否存在點D,使得△BDE和△ACE相似?若存在,請求出點D的坐標,若不存在,請說明理由;
(3)如圖2,F是第一象限內拋物線上的動點(不與點D重合),點G是線段AB上的動點.連接DF,FG,當四邊形DEGF是平行四邊形且周長最大時,請直接寫出點G的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=![]() x12的圖象分別交x軸,y軸于A,C兩點。
x12的圖象分別交x軸,y軸于A,C兩點。
(1)求出A,C兩點的坐標;
(2)在x軸上找出點B,使△ACB∽△AOC,若拋物線過A,B,C三點,求出此拋物線的解析式;
(3)在(2)的條件下,設動點P、Q分別從A,B兩點同時出發,以相同速度沿AC、BA向C,A運動,連接PQ,設AP=m,是否存在m值,使以A,P,Q為頂點的三角形與△ABC相似?若存在,求出所有m值;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
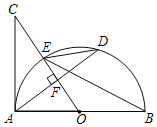
【題目】如圖,AB是半圓O的直徑,點C圓外一點,OC垂直于弦AD,垂足為點F,OC交⊙O于點E,連接AC,∠BED=∠C.
(1)判斷AC與⊙O的位置關系,并證明你的結論;
(2)是否存在BE平分∠OED的情況?如果存在,求此時∠C的度數;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在大樓AB正前方有一斜坡CD,坡角∠DCE=30°,樓高AB=60米,在斜坡下的點C處測得樓頂B的仰角為60°,在斜坡上的D處測得樓頂B的仰角為45°,其中點A,C,E在同一直線上.
(1)求坡底C點到大樓距離AC的值;
(2)求斜坡CD的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AC與⊙O交于點F,弦AD平分∠BAC,DE⊥AC,垂足為E點.
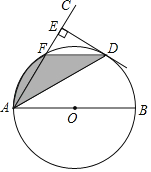
(1)求證:DE是⊙O的切線;
(2)若⊙O的半徑為2,∠BAC=60°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】求證:三角形的中位線平行于三角形的第三邊,并且等于第三邊的一半.解答要求如下:
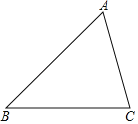
(1)對于圖中△ABC,用尺規作出一條中位線DE;(不必寫作法,但應保留作圖痕跡)
(2)根據(1)中作出的中位線,寫出已知,求證和證明過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com