
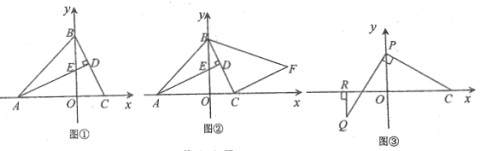
【題目】在平面直角坐標系中,![]() 的頂點
的頂點![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 軸于點
軸于點![]()
(1)如圖①,求點![]() 的坐標;
的坐標;
(2)如圖②:將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后得線段
后得線段![]() ,連接
,連接![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)如圖③, 點![]() 為
為![]() 軸正半軸上一動點, 點
軸正半軸上一動點, 點![]() 在第二象限內,
在第二象限內,![]() 于
于![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 垂直
垂直![]() 軸于點
軸于點![]() ,求
,求![]() 的值.
的值.
 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中(如圖),已知點A在x軸的正半軸上,且與原點的距離為3,拋物線y=ax2﹣4ax+3(a≠0)經過點A,其頂點為C,直線y=1與y軸交于點B,與拋物線交于點D(在其對稱軸右側),聯結BC、CD.
(1)求拋物線的表達式及點C的坐標;
(2)點P是y軸的負半軸上的一點,如果△PBC與△BCD相似,且相似比不為1,求點P的坐標;
(3)將∠CBD繞著點B逆時針方向旋轉,使射線BC經過點A,另一邊與拋物線交于點E(點E在對稱軸的右側),求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數![]() (k≠0)的圖像與一次函數y=-x+b的圖像在第一象限交于A、B兩點,BC⊥x軸于點C,若△OBC的面積為2,且A點的縱坐標為4,B點的縱坐標為1.
(k≠0)的圖像與一次函數y=-x+b的圖像在第一象限交于A、B兩點,BC⊥x軸于點C,若△OBC的面積為2,且A點的縱坐標為4,B點的縱坐標為1.
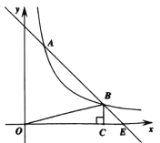
(1)求反比例函數、一次函數的表達式及直線AB與x軸交點E的坐標;
(2)已知點D(t,0)(t>0),過點D作垂直于x軸的直線,在第一象限內與一次函數y=-x+b的圖像相交于點P,與反比函數![]() 上的圖像相交于點Q,若點P位于點Q的上方,請結合函數圖像直接寫出此時t的取值范圍.
上的圖像相交于點Q,若點P位于點Q的上方,請結合函數圖像直接寫出此時t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
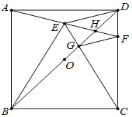
【題目】如圖,正方形ABCD中,O為BD中點,以BC為邊向正方形內作等邊△BCE,連接AE并延長交CD于F,連接BD分別交CE、AF于G、H,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() :
:![]() ,其中正確的是__________.
,其中正確的是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
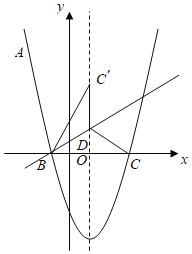
【題目】如圖,拋物線![]() 經過點
經過點![]() ,與
,與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,
兩點,
(1)拋物線的函數表達式;
(2)點![]() 在拋物線的對稱軸上,且位于
在拋物線的對稱軸上,且位于![]() 軸的上方,將
軸的上方,將![]() 沿沿直線
沿沿直線![]() 翻折得到
翻折得到![]() ,若點
,若點![]() 恰好落在拋物線的對稱軸上,求點
恰好落在拋物線的對稱軸上,求點![]() 和點
和點![]() 的坐標;
的坐標;
(3)設![]() 是拋物線上位于對稱軸右側的一點,點
是拋物線上位于對稱軸右側的一點,點![]() 在拋物線的對稱軸上,當
在拋物線的對稱軸上,當![]() 為等邊三角形時,求直線
為等邊三角形時,求直線![]() 的函數表達式.
的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
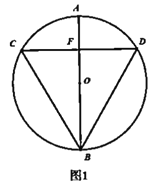
【題目】已知,![]() 是⊙O的直徑,弦
是⊙O的直徑,弦![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,連接
,連接![]() .
.
(1)如圖1,求![]() 的度數;
的度數;
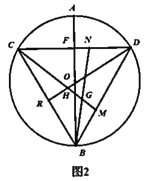
(2)如圖2,點![]() 分別為
分別為![]() 上一點,并且
上一點,并且![]() ,連接
,連接![]() ,交點為G,R為
,交點為G,R為![]() 上一點,連接
上一點,連接![]() 與
與![]() 交于點H,
交于點H,![]() ,求證:
,求證:![]() ;
;
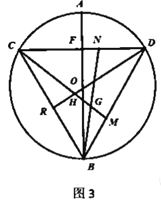
(3)如圖3,在(2)的條件下,![]() ,求⊙O半徑.
,求⊙O半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是一款“雷達式”懶人椅.當懶人椅完全展開時,其側面示意圖如圖2所示,金屬桿AB、CD在點O處連接,且分別與金屬桿EF在點B,D處連接.金屬桿CD的OD部分可以伸縮(即OD的長度可變).已知OA=50cm,OB=20cm,OC=30cm.DE=BF=5cm.當把懶人椅完全疊合時,金屬桿AB,CD,EF重合在一條直線上(如圖3所示),此時點E和點A重合.
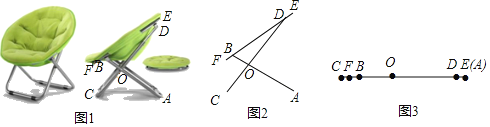
(1)如圖2,已知∠BOD=6∠ODB,∠OBF=140°.
①求∠AOC的度數.
②求點A,C之間的距離.
(2)如圖3,當懶人椅完全疊合時,求CF與CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市中學生參加“科普知識”競賽成績的情況,隨機抽查了部分參賽學生的成績,作出如圖所示的統計圖和統計表.請根據圖表信息,解答下列問題:
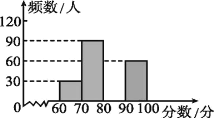

(1)在表中:m= ,n= ;在圖中補全頻數分布直方圖;
(2)小明的成績是所有被抽查學生成績的中位數,據此推斷他的成績在 組;
(3)4個小組每組推薦1人,然后從4人中隨機抽取2人參加頒獎典禮,恰好抽中A、C兩組學生的概率是多少?請用列表法或畫樹狀圖法說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某課外學習小組根據學習函數的經驗,對函數![]() 的圖象與性質進行了探究請補充完整以下探索過程:
的圖象與性質進行了探究請補充完整以下探索過程:
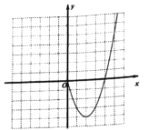
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接寫出![]() ________,
________,![]() ________;
________;
(2)根據上表中的數據,在平面直角坐標系內補全該函數的圖象,并結合圖象寫出該函數的兩條性質:
性質1______________________________________________________
性質2_______________________________________________________
(3)若方程![]() 有四個不同的實數根,請根據函數圖象,直接寫出k的取值范圍.
有四個不同的實數根,請根據函數圖象,直接寫出k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com