
【題目】(1)問題背景:
如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分別是BC,CD上的點,且∠EAF=60°,探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是延長FD到點G,使DG=BE,連結AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結論,他的結論應是 ;

(2)探索延伸:
如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°,E,F分別是BC,CD上的點,且∠EAF=![]() ∠BAD,上述結論是否仍然成立,并說明理由;
∠BAD,上述結論是否仍然成立,并說明理由;
(3)結論應用:
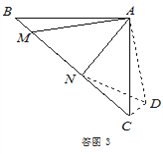
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西30°的A處,艦艇乙在指揮中心南偏東70°的B處,并且兩艦艇到指揮中心的距離相等.接到行動指令后,艦艇甲向正東方向以60海里/小時的速度前進,艦艇乙沿北偏東50°的方向以80海里/小時的速度前進,1.5小時后,指揮中心觀測到甲、乙兩艦艇分別到達E,F處,且兩艦艇與指揮中心O之間夾角∠EOF=70°,試求此時兩艦艇之間的距離.
(4)能力提高:
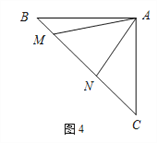
如圖4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,點M,N在邊BC上,且∠MAN=45°.若BM=1,CN=3,試求出MN的長.
【答案】(1)EF=BE+FD;(2)EF=BE+FD仍然成立;(3)210;(4)MN=![]() .
.
【解析】試題分析:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;(2)延長FD到點G,使DG=BE,連接AG,證明△ABE≌△ADG,再證△AEF≌△AGF,得EF=FG,即可得到答案;(3)連接EF,延長AE,BF相交于點C,根據探索延伸可得EF=AE+FB,即可計算出EF的長度;(4)在△ABC外側作∠CAD=∠BAM,截取AD=AM,連接CD,DN,證明△ACD≌△ABM,得到CD=BM,再證MN=ND,則求出ND的長度,即可得到答案.
解:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;
(2)EF=BE+FD仍然成立.
證明:如答圖1,延長FD到點G,使DG=BE,連接AG,
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,∴∠B=∠ADG,
在△ABE與△ADG中,AB=AD,∠B=∠ADG,BE=DG,∴△ABE≌△ADG.
∴AE=AG,∠BAE=∠DAG.
又∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD-∠EAF=∠BAD-![]() ∠BAD=
∠BAD=![]() ∠BAD,
∠BAD,
∴∠EAF=∠GAF.
在△AEF與△AGF中,AE=AG,∠EAF=∠GAF,AF=AF,
∴△AEF≌△AGF.∴EF=FG.
又∵FG=DG+DF=BE+DF.
∴EF=BE+FD.
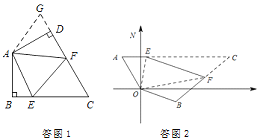
(3)如答圖2,連接EF,延長AE,BF相交于點C,在四邊形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°=![]() ∠AOB,
∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的條件,
∴結論EF=AE+FB成立.
∴EF=AE+FB=1.5×(60+80)=210(海里).
答:此時兩艦艇之間的距離為210海里;
(4)如答圖3,在△ABC外側作∠CAD=∠BAM,截取AD=AM,連接CD,DN,
在△ACD與△ABM中,AC=AB,∠CAD=∠BAM,AD=AM,
則△ACD≌△ABM,∴CD=BM=1,∠ACD=∠ABM=45°,
∵∠NAD=∠NAC+∠CAD=∠NAC+∠BAM=∠BAC-∠MAN=45°,
∴∠MAD=∠MAN+∠NAD=90°=2∠NAD,
又∵AM=AD,∠NCD+∠MAD=(∠ACD+∠ACB)+90°=180°,
∴對于四邊形AMCD符合探索延伸,
則ND=MN,
∵∠NCD=90°,CD=1,CN=3,
∴MN=ND=![]() .
.


科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數 ![]() 的圖象與性質.小懷根據學習函數的經驗,對函數
的圖象與性質.小懷根據學習函數的經驗,對函數 ![]() 的圖象與性質進行了探究.下面是小懷的探究過程,請補充完成:
的圖象與性質進行了探究.下面是小懷的探究過程,請補充完成:
(1)函數 ![]() 的自變量x的取值范圍是;
的自變量x的取值范圍是;
(2)列出y與x的幾組對應值.請直接寫出m的值,m=;
(3)請在平面直角坐標系xOy中,描出以上表中各對對應值為坐標的點,并畫出該函數的圖象;
(4)結合函數的圖象,寫出函數 ![]() 的一條性質.
的一條性質.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣ | ﹣ | 0 | 1 | 2 | m | 4 | 5 | … |
y | … | | | | 2 | 3 | ﹣1 | 0 | | | | | | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次課題學習中,老師讓同學們合作編題.某學習小組受趙爽弦圖的啟發,編寫了下面這道題,請你來解一解.
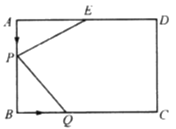
如圖,將矩形ABCD的四邊BA、CB、DC、AD分別延長至E、F、G、H,使得AE=CG,BF=DH,連結EF、FG、GH、HE.
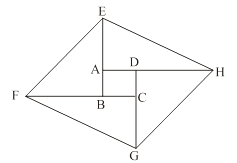
(1)求證:四邊形EFGH為平行四邊形;
(2)若矩形ABCD是邊長為1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,△ABC是等邊三角形,點D、E分別是邊BC、CA上的點,且BD=CE,AD、BE相交于點O.
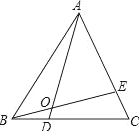
(1)求證:△BAE≌△ACD;
(2)求∠AOB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形![]() 中,
中,![]() cm,
cm,![]() cm,點
cm,點![]() 為
為![]() 的中點.若點
的中點.若點![]() 在線段
在線段![]() 上以1 cm/s的速度由點
上以1 cm/s的速度由點![]() 向點
向點![]() 運動,到點
運動,到點![]() 時不動.同時,點
時不動.同時,點![]() 在線段
在線段![]() 上由點
上由點![]() 向點
向點![]() 運動.
運動.
(1)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,經過1 s后,
的運動速度相等,經過1 s后,![]() 與
與![]() 是否全等?請說明理由,并判斷此時線段
是否全等?請說明理由,并判斷此時線段![]() 和
和![]() 的位置關系;
的位置關系;
(2)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,運動時間為
的運動速度相等,運動時間為![]() s,設
s,設![]() 的面積為
的面積為![]() cm2,請用含
cm2,請用含![]() 的代數式表示
的代數式表示
(3)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度不相等,當點
的運動速度不相等,當點![]() 的運動速度為多少時,能夠使
的運動速度為多少時,能夠使![]() 與
與![]() 全等?
全等?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題9分)把代數式通過配湊等手段,得到完全平方式,再運用完全平方式是非負性這一性質增加問題的條件,這種解題方法叫做配方法.配方法在代數式求值,解方程,最值問題等都有著廣泛的應用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴當a=b=1時,M有最小值1
請根據上述材料解決下列問題:
(1)在橫線上添上一個常數項使之成為完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的角平分線,DF⊥AB,垂足為F,DE=DG,△ADG和△AED的面積分別為40和28,則△EDF的面積為( )
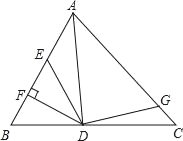
A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下列數組作為三角形的三條邊長,其中能構成直角三角形的是( )
A. 1, ![]() ,3 B.
,3 B. ![]() ,
, ![]() ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. ![]() ,
, ![]() ,
, ![]()
【答案】C
【解析】A、12+(![]() )2≠32,不能構成直角三角形,故選項錯誤;
)2≠32,不能構成直角三角形,故選項錯誤;
B、(![]() 2+(
2+(![]() )2≠52,不能構成直角三角形,故選項錯誤;
)2≠52,不能構成直角三角形,故選項錯誤;
C、1.52+22=2.52,能構成直角三角形,故選項正確;
D、(![]() ))2+(
))2+(![]() )2≠(
)2≠(![]() )2,不能構成直角三角形,故選項錯誤.
)2,不能構成直角三角形,故選項錯誤.
故選:C.
【題型】單選題
【結束】
3
【題目】在Rt△ABC中,∠C=90°,AC=9,BC=12,則點C到斜邊AB的距離是( )
(A)![]() (B)
(B)![]() (C)9 (D)6
(C)9 (D)6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com