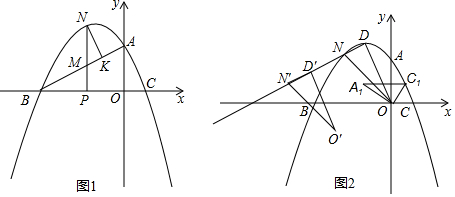10.如圖,在平面直角坐標系中,拋物線y=-$\frac{\sqrt{3}}{3}$x
2+bx+c與x軸交于B、C兩點(點B在點C的左側),與y軸交于點A,拋物線的頂點為D,B(-3,0),A(0,$\sqrt{3}$)
((1)求拋物線解析式及D點坐標;
(2)如圖1,P為線段OB上(不與O、B重舍)一動點,過點P作y軸的平行線交線段AB于點M,交拋物線于點N,點N作NK⊥BA交BA于點K,當△MNK與△MPB的面積相等時,在X軸上找一動點Q,使得$\frac{1}{2}$CQ+QN最小時,求點Q的坐標及$\frac{1}{2}$CQ+QN最小值;
(3)如圖2,在(2)的條件下,將△ODN沿射線DN平移,平移后的對應三角形為△O′D′N′,將△AOC繞點O逆時針旋轉到A
1OC
1的位置,且點C
1恰好落在AC上,△A
1D′N′是否能為等腰三角形,若能求出N′的坐標,若不能,請說明理由.
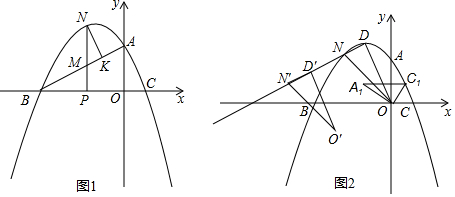

 名校課堂系列答案
名校課堂系列答案