如圖，在平面直角坐標系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜邊都在坐標軸上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°．若點A1的坐標為（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，則依此規律，點A2014的縱坐標為（ ）
|
| A． | 0 | B． | ﹣3×（ | C． | （2 | D． | 3×（ |
科目：初中數學 來源： 題型：
對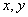
定義一種新運算
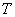，規定：
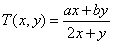（其中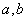
均為非零常數），這里等式右邊是通常的四則運算，例如：
。
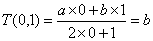（1）已知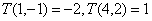
①求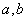的值；
②若關于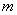
的不等式組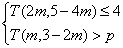
恰好有3個整數解，求實數
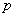的取值范圍；
（2）若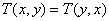
對任意實數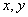都成立（這里
，
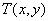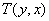都有意義），則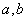應滿足怎樣的關系式？
查看答案和解析>>
科目：初中數學 來源： 題型：
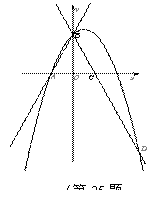
如圖，直線y=2x+2與x軸交于點A，與y軸交于點B．把△AOB沿y
軸翻折，點A落到點C，過點B的拋物線
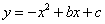與直線BC交于點D（3，
）．
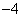（1）求直線BD和拋物線的解析式；
（2）在第一象限內的拋物線上，是否存在一點M，作MN垂直于x軸，垂足為點N，使得以M、O、N為頂點的三角形與△BOC相似？若存在，求出點M的坐標；若不存在，請說明理由；
（3）在直線BD上方的拋物線上有一動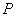點
，過點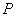作PH垂直于x軸，交直線BD于點
．當四邊形
是平行四邊形時，試求動點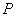的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
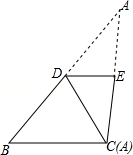
如圖，有一直角三角形紙片ABC，邊BC=6，AB=10，∠ACB=90°，將該直角三角形紙片沿DE折疊，使點A與點C重合，則四邊形DBCE的周長為 18 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
猜想與證明：
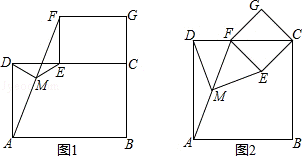
如圖1擺放矩形紙片ABCD與矩形紙片ECGF，使B、C、G三點在一條直線上，CE在邊CD上，連接AF，若M為AF的中點，連接DM、ME，試猜想DM與ME的關系，并證明你的結論．
拓展與延伸：
（1）若將”猜想與證明“中的紙片換成正方形紙片ABCD與正方形紙片ECGF，其他條件不變，則DM和ME的關系為 ．
（2）如圖2擺放正方形紙片ABCD與正方形紙片ECGF，使點F在邊CD上，點M仍為AF的中點，試證明（1）中的結論仍然成立．
查看答案和解析>>
科目：初中數學 來源： 題型：
已知當x1=
a，x2=b，x3=c時，二次函數y=
x2+mx對應的函數值分別為y1，y2，y3，若正整數a，b，c恰好是一個三角形的三邊長，且當a＜b＜c時，都有y1＜y2＜y3，則實數m的取值范圍是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
）2013
）2014
）2013
的圖象與
軸只有一個交點，那么
的值為( )
m的竹竿的影長為3m，同時測得一根旗桿的影長為25m，那么這根旗桿的高度為 m．