
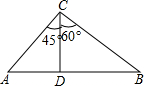
 如圖,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB.
如圖,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB. 分析 根據(jù)在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,可以求得∠CDA=∠CDB=90°,從而可以求得各邊的長,本題得以解決.
解答 解:∵在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,
∴∠CDA=∠CDB=90°,∠CAD=45°,∠B=30°,
∴CD=AD,BC=2CD,
∵AC=$40\sqrt{2}$,CD2+AD2=AC2,
∴CD=AD=$\sqrt{\frac{A{C}^{2}}{2}}=\sqrt{\frac{(40\sqrt{2})^{2}}{2}}$=40,
∴BC=80,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}=\sqrt{8{0}^{2}-4{0}^{2}}=40\sqrt{3}$,
∴AB=AD+BD=40+40$\sqrt{3}$,
即AB的長是40+40$\sqrt{3}$.
點評 本題考查解直角三角形,解題的關(guān)鍵是明確各邊之間的關(guān)系,由題目中的信息求出各邊的長,然后找出所求問題需要的條件.


 探究與鞏固河南科學(xué)技術(shù)出版社系列答案
探究與鞏固河南科學(xué)技術(shù)出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
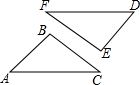 如圖,△ABC≌△DEF,∠A=50°,∠B=100°,則∠F的度數(shù)是( )
如圖,△ABC≌△DEF,∠A=50°,∠B=100°,則∠F的度數(shù)是( )| A. | 30° | B. | 50° | C. | 60° | D. | 100° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 14 | 4 | -2 | -4 | -2 | 4 | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 任意打開一本200頁的數(shù)學(xué)書,恰好是第50頁 | |
| B. | 打開電視機,任選一個頻道,正在播放足球賽 | |
| C. | 在空曠的操場上向上拋出的籃球一定會下落 | |
| D. | 陰天一定會下雨 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com