
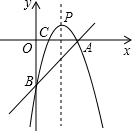
 如圖,直線y=x-3與x軸、y軸分別相交于點A,B,經過A,B兩點的拋物線y=-x2+bx+c與x軸的另一個交點為C.
如圖,直線y=x-3與x軸、y軸分別相交于點A,B,經過A,B兩點的拋物線y=-x2+bx+c與x軸的另一個交點為C.分析 (1)先求A、B兩點的坐標,利用待定系數法求二次函數的解析式,在令y=0解一元二次方程求方程的解,從而求出點C的坐標;
(2)根據軸對稱的最短路徑找到點E:直線AB與對稱軸的交點即是E點,求直線AB的解析式,再求與對稱軸的交點坐標即可;
(3)分兩種情況計算:點F分別在x軸的上方和下方,根據等角的三角函數列式計算即可.
解答 解:(1)當x=0時,y=3,
當y=0時,x-3=0,x=3,
∴A(3,0),B(0,-3),
把A(3,0),B(0,-3)代入拋物線y=-x2+bx+c中得:
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=-3}\end{array}\right.$,
∴拋物線的解析式為:y=-x2+4x-3,
當y=0時,-x2+4x-3=0,
x1=1,x2=3,
∴C(1,0),
(2)y=-x2+4x-3=-(x-2)2+1,
∴P(2,1),
∵C、A關于拋物線的對稱軸對稱,
∴直線AB與對稱軸的交點即為點E,
如圖1,此時EB+EC為最小,
當x=2時,y=2-3=-1,
∴E(2,-1);
(3)過F作FD⊥x軸于D,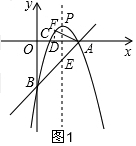
設F(a,-a2+4a-3),
∵∠FAO=∠OBC,∠BOC=∠FDA=90°,
∴△BOC∽△ADF,
∴$\frac{OC}{OB}=\frac{FD}{AD}$,
∵C(1,0),B(0,-3),
∴OC=1,OB=3,
當F在x軸的上方時,如圖1,
得$\frac{-{a}^{2}+4a-3}{3-a}$=$\frac{1}{3}$,
3-a=-3a2+12a-9,
3a2-13a+12=0,
(a-3)(3a-4)=0,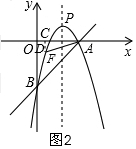
a1=3(舍),a2=$\frac{4}{3}$,
∴F($\frac{4}{3}$,$\frac{5}{9}$),
當F在x軸的下方時,如圖2,
得$\frac{{a}^{2}-4a+3}{3-a}$=$\frac{1}{3}$,
解得:x1=3(舍),x2=$\frac{2}{3}$,
∴F($\frac{2}{3}$,-$\frac{7}{9}$),
綜上所述,點F的坐標為($\frac{4}{3}$,$\frac{5}{9}$)或($\frac{2}{3}$,-$\frac{7}{9}$).
點評 本題主要考查待定系數法、軸對稱的最短路徑問題、方程、函數及三角形相似等知識,也考查了綜合運用數學知識、分析問題、解決問題的能力以及數形結合、分類討論的思想,是常考題型,正確運用分類討論是解題關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,設四邊形ABCD是邊長為1的正方形,以對角線AC為邊作第2個正方形ACEF,再以對角線AE為邊作第3個正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )
如圖,設四邊形ABCD是邊長為1的正方形,以對角線AC為邊作第2個正方形ACEF,再以對角線AE為邊作第3個正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,?ABOC如圖放置,點C的坐標是(-1,0),點A在y軸的正半軸上,將此平行四邊形繞點O順時針旋轉90°,得?A′B′OC′,拋物線y=ax2+bx+4過點C、A、A′,點M是此拋物線的一動點,設點M的橫坐標為m.
在平面直角坐標系中,?ABOC如圖放置,點C的坐標是(-1,0),點A在y軸的正半軸上,將此平行四邊形繞點O順時針旋轉90°,得?A′B′OC′,拋物線y=ax2+bx+4過點C、A、A′,點M是此拋物線的一動點,設點M的橫坐標為m.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com