
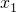 ,
,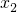 ,
,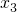 ,…,
,…,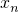 的平均數是
的平均數是 ,方差是
,方差是 ,則數據是
,則數據是 +1,
+1,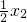 +1,
+1,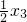 +1,…,
+1,…,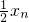 +1的平均數是________,方差是________.
+1的平均數是________,方差是________.
 +1
+1  S2
S2 ,方差是s2,則另一組數據
,方差是s2,則另一組數據 +1,
+1,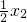 +1,
+1,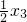 +1,…,
+1,…,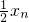 +1的平均數為
+1的平均數為 
 +1,方差是s′2,代入方差的公式S2=
+1,方差是s′2,代入方差的公式S2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],計算即可.
)2],計算即可.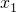 ,
,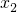 ,
,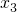 ,…,
,…,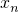 的平均數是
的平均數是 ,方差是
,方差是 ,
, +1,
+1,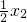 +1,
+1,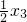 +1,…,
+1,…,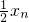 +1的平均數為
+1的平均數為
 +1,方差是s′2,
+1,方差是s′2, [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],
)2], [(
[( x1+1-
x1+1-
 -1)2+(
-1)2+( x2+1-
x2+1-
 -1)2+…+(
-1)2+…+( xn+1-
xn+1-
 -1)2]
-1)2] [
[ (x1-
(x1- )2+
)2+ (x2-
(x2- )2+…+
)2+…+ (xn-
(xn- )2],
)2], S2.
S2.
 +1,
+1, S2.
S2.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com