av免费在线播放,成人精品久久久,操久久

【題目】如圖，已知⊙O為四邊形ABCD的外接圓，O為圓心，若∠BCD=120°，AB=AD=2，則⊙O的半徑長為（）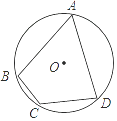

A.
B.
C.
D.

【答案】D
【解析】解：連接BD，作OE⊥AD，連接OD，

∵⊙O為四邊形ABCD的外接圓，∠BCD=120°，
∴∠BAD=60°．
∵AD=AB=2，
∴△ABD是等邊三角形．
∴DE= AD=1，∠ODE= ∠ADB=30°，
∴OD= = ．
答案為：D．
【考點精析】利用垂徑定理和圓內接四邊形的性質對題目進行判斷即可得到答案，需要熟知垂徑定理：平分弦（不是直徑）的直徑垂直于弦，并且平分弦所對的兩條弧；把圓分成n(n≥3):1、依次連結各分點所得的多邊形是這個圓的內接正n邊形2、經過各分點作圓的切線，以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形．

練習冊系列答案

悅文圖書高考必贏系列叢書快樂寒假延邊人民出版社系列答案

贏在假期搶分計劃寒假合肥工業大學出版社系列答案

贏在假期期末加寒假合肥工業大學出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

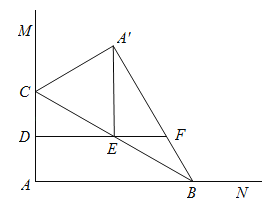
【題目】如圖，在ABCD中過點A作AE⊥DC，垂足為E，連接BE，F為BE上一點，且∠AFE=∠D．

（1）求證：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD= ，求AF的長．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，點在邊上，點為邊上一動點，連接與關于所在直線對稱，點分別為的中點，連接并延長交所在直線于點，連接．當為直角三角形時，的長為_________ ．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】類比思想就是根據已經學習過的知識，類比探究新知識的思想方法．我們在探究矩形、菱形、正方形等問題中的數量關系時，經常用到類比思想．某數學興趣小組在數學課外活動中，研究三角形和正方形的性質時，做了如下探究：在中，點為直線上一動點(點不與重合)，以為邊在右側作正方形連接．

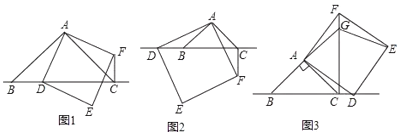
（1）（觀察猜想）如圖①，當點在線段上時；

①與的位置關系為：；

②之間的數量關系為：；(將結論直接寫在橫線上)

（2）（數學思考）如圖②，當點在線段的延長線上時，結論①②是否仍然成立？若成立，請給予證明；若不成立，請你寫出正確結論再給予證明；

（3）（拓展延伸）如圖③，當點在線段的延長線上時，延長交于點，連接．若已知請直接寫出的長．(提示：．過作于過作于于)

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，已知AB∥EF，∠C＝90°，∠B，∠D，∠E三個角的大小分別是x，y，z則x，y，z之間滿足的關系式是(　　)

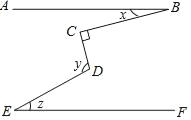
A. x+z＝yB. x+y+═180°C. x+y﹣z＝90°D. y+z﹣x＝180°

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，四邊形ABCD內接于⊙O，∠BAD=90°， = ，過點C作CE⊥AD，垂足為E，若AE=3，DE= ，求∠ABC的度數．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】已知：∠MON=36°，OE平分∠MON，點A，B分別是射線OM，OE，上的動點（A，B不與點O重合），點D是線段OB上的動點，連接AD并延長交射線ON于點C，設∠OAC=x，

（1）如圖1，若AB∥ON，則

①∠ABO的度數是______；

②當∠BAD=∠ABD時，x=______；

當∠BAD=∠BDA時，x=______；

（2）如圖2，若AB⊥OM，則是否存在這樣的x的值，使得△ABD中有兩個相等的角？若存在，求出x的值；若不存在，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，地面上小山的兩側有A，B兩地，為了測量A，B兩地的距離，讓一熱氣球從小山西側A地出發沿與AB成30°角的方向，以每分鐘40m的速度直線飛行，10分鐘后到達C處，此時熱氣球上的人測得CB與AB成70°角，請你用測得的數據求A，B兩地的距離AB長．（結果用含非特殊角的三角函數和根式表示即可）