
【題目】如圖,在ABCD中 過點A作AE⊥DC,垂足為E,連接BE,F為BE上一點,且∠AFE=∠D.
(1)求證:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD= ![]() ,求AF的長.
,求AF的長.
【答案】
(1)證明:∵四邊形ABCD是平行四邊形,∴AB∥CD,AD∥BC,AD=BC,
∴∠D+∠C=180°,∠ABF=∠BEC,∵∠AFB+∠AFE=180°,∴∠C=∠AFB,∴△ABF∽△BEC
(2)解:∵AE⊥DC,AB∥DC,∴∠AED=∠BAE=90°,
在Rt△ABE中,根據勾股定理得:BE= ![]() ,
,
在Rt△ADE中,AE=ADsinD=5× ![]() =4,∵BC=AD=5,
=4,∵BC=AD=5,
由(1)得:△ABF∽△BEC,∴ ![]() ,即
,即 ![]() ,解得:AF=2
,解得:AF=2 ![]()
【解析】由平行四邊形的性質得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,證出∠C=∠AFB,即可得出結論;
由三角函數求出AE,由勾股定理求出BE,再由相似三角形的性質求出AF的長.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】隨著我國經濟的高速發展,有著“經濟晴雨表”之稱的股市也得到迅速的發展,下表是今年上證指數某一周星期一至星期五的變化情況. (注:上周五收盤時上證指數為2616點,每一天收盤時指數與前一天相比,漲記為“+”,跌記為“-”)
星 期 | 一 | 二 | 三 | 四 | 五 |
指數的變化(與前一天比較) |
|
|
|
|
|
⑴ 請求出這一周星期五收盤時的上證指數是多少點?
⑵ 說出這一周每一天收盤時上證指數哪一天最高?哪一天最低?分別是多少點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一批單價為20元的商品,若每件按30元的價格銷售時,每天能賣出60件;若每件按50元的價格銷售時,每天能賣出20件,假定每天銷售件數y(件)與銷售價格x(元/件)滿足y=kx+b.
(1)求y與x滿足的函數關系式(不要求寫出x的取值范圍);
(2)在不考慮其他因素的情況下,每件商品銷售價格定為多少元時才能使每天獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在橫線上完成下面的證明,并在括號內注明理由.
已知:如圖,∠ABC+∠BGD=180°,∠1=∠2.
求證:EF∥DB.
證明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有大小兩種貨車,已知1輛大貨車與3輛小貨車一次可以運貨14噸,2輛大貨車與5輛小貨車一次可以運貨25噸.
(1)1輛大貨車與1輛小貨車一次可以運貨各多少噸?
(2)1輛大貨車一次費用為300元,1輛小貨車一次費用為200元,要求兩種貨車共用10輛,兩次完成80噸的運貨任務,且總費用不超過5400元,有哪幾種用車方案?請指出費用最低的一種方案,并求出相應的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元宵節將至,我校組織學生制作并選送50盞花燈,共包括傳統花燈、創意花燈和現代花燈三大種.已知每盞傳統花燈需要35元材料費,每盞創意花燈需要33元材料費,每盞現代花燈需要30元材料費.
(1)如果我校選送20盞現代花燈,已知傳統花燈數量不少于5盞且總材料費不得超過1605元,請問選送傳統花燈、創意花燈的數量有哪幾種方案?
(2)當三種花燈材料總費用為1535元時,求選送傳統花燈、創意花燈、現代花燈各幾盞?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是反比例函數 ![]() 的圖象上的一個動點,連接OA,若將線段O A繞點O順時針旋轉90°得到線段OB,則點B所在圖象的函數表達式為 .
的圖象上的一個動點,連接OA,若將線段O A繞點O順時針旋轉90°得到線段OB,則點B所在圖象的函數表達式為 . 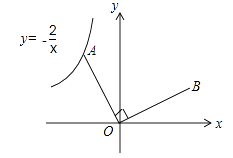
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com