
【題目】類比思想就是根據已經學習過的知識,類比探究新知識的思想方法.我們在探究矩形、菱形、正方形等問題中的數量關系時,經常用到類比思想.某數學興趣小組在數學課外活動中,研究三角形和正方形的性質時,做了如下探究:在![]() 中,
中,![]() 點
點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與
不與![]() 重合),以
重合),以![]() 為邊在
為邊在![]() 右側作正方形
右側作正方形![]() 連接
連接![]() .
.
(1)(觀察猜想)如圖①,當點![]() 在線段
在線段![]() 上時;
上時;
①![]() 與
與![]() 的位置關系為: ;
的位置關系為: ;
②![]() 之間的數量關系為: ;(將結論直接寫在橫線上)
之間的數量關系為: ;(將結論直接寫在橫線上)
(2)(數學思考)如圖②,當點![]() 在線段
在線段![]() 的延長線上時,結論①②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
的延長線上時,結論①②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
(3)(拓展延伸)如圖③,當點![]() 在線段
在線段![]() 的延長線上時,延長
的延長線上時,延長![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .若已知
.若已知![]() 請直接寫出
請直接寫出![]() 的長.(提示: .過
的長.(提示: .過![]() 作
作![]() 于
于![]() 過
過![]() 作
作![]() 于
于![]() 于
于![]() )
)
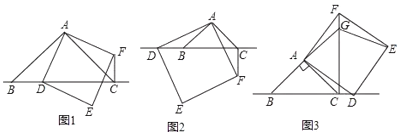
【答案】(1)①垂直;![]()
![]() ;(2)結論①成立;結論②不成立,正確結論為:
;(2)結論①成立;結論②不成立,正確結論為:![]() .理由見解析;(3)
.理由見解析;(3)![]() .
.
【解析】
(1)根據正方形的性質得到![]() ,推出
,推出![]() ,根據全等三角形的性質即可得到結論;由正方形
,根據全等三角形的性質即可得到結論;由正方形![]() 的性質可推出
的性質可推出![]() ,根據全等三角形的性質得到
,根據全等三角形的性質得到![]() ,
,![]() ,根據余角的性質即可得到結論;
,根據余角的性質即可得到結論;
(2)根據正方形的性質得到![]() ,推出
,推出![]() ,根據全等三角形的性質以及等腰直角三角形的角的性質可得到結論.
,根據全等三角形的性質以及等腰直角三角形的角的性質可得到結論.
(3)過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,如圖3所示,由
,如圖3所示,由![]() ,推出
,推出![]() ,
,![]() ,推出
,推出![]() ,
,![]() ,由
,由![]() 是等腰直角三角形,推出
是等腰直角三角形,推出![]() ,推出
,推出![]() ,再由勾股定理即可解決問題.
,再由勾股定理即可解決問題.
解:(1)①在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 與
與![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ;
;
故答案為:![]() ;
;
②由①知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
故答案為:![]() ;
;
(2)![]() 成立;
成立;![]() 不成立,新結論為:
不成立,新結論為:![]() .理由如下:
.理由如下:
在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 與
與![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
(3)解:如圖3,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
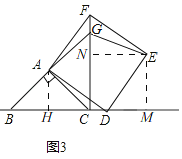
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在正方形![]() 中,
中,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
在![]() 與
與![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
![]() ,
,![]() ,
,
![]() 四邊形
四邊形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() .
.


科目:初中數學 來源: 題型:
【題目】在橫線上完成下面的證明,并在括號內注明理由.
已知:如圖,∠ABC+∠BGD=180°,∠1=∠2.
求證:EF∥DB.
證明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是反比例函數 ![]() 的圖象上的一個動點,連接OA,若將線段O A繞點O順時針旋轉90°得到線段OB,則點B所在圖象的函數表達式為 .
的圖象上的一個動點,連接OA,若將線段O A繞點O順時針旋轉90°得到線段OB,則點B所在圖象的函數表達式為 . 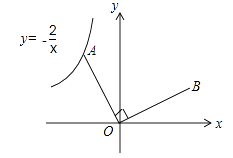
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠1=∠2,G為AD的中點,BG的延長線交AC于點E,F為AB上的一點,CF與AD垂直,交AD于點H,則下面判斷正確的有( )

①AD是△ABE的角平分線;②BE是△ABD的邊AD上的中線;
③CH是△ACD的邊AD上的高;④AH是△ACF的角平分線和高
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,給出以下結論:①
,給出以下結論:①![]() 為等腰直角三角形;②
為等腰直角三角形;②![]() 為等邊三角形;③
為等邊三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位線.其中正確的結論有( )
的中位線.其中正確的結論有( )
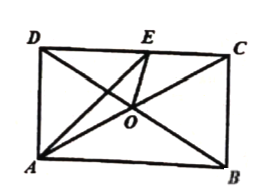
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區果農收獲草莓30噸,枇杷13噸,現計劃租用甲、乙兩種貨車共10輛將這批水果全部運往省城,已知甲種貨車可裝草莓4噸和枇杷1噸,乙種貨車可裝草莓、枇杷各2噸.
(1)該果農安排甲、乙兩種貨車時有幾種方案請您幫助設計出來;
(2)若甲種貨車每輛要付運輸費2 000元,乙種貨車每輛要付運輸費1 300元,則該果農應選擇哪種運輸方案才能使運費最少,最少運費是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,把矩形![]() 放在平面直角坐標系中,邊
放在平面直角坐標系中,邊![]() 在
在![]() 軸上,邊
軸上,邊![]() 在
在![]() 軸上,連接
軸上,連接![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 平分
平分![]() 交
交![]() 于點
于點![]() .動點
.動點![]() 在線段
在線段![]() 上運動,過
上運動,過![]() 作
作![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() .
.
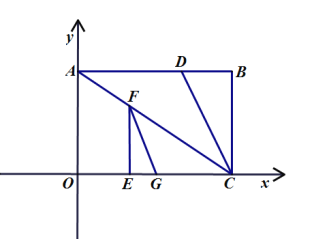
(1)當![]() 時,在線段
時,在線段![]() 上有一動點
上有一動點![]() ,
,![]() 軸上有一動點
軸上有一動點![]() ,連接
,連接![]() 當
當![]() 周長最小時,求
周長最小時,求![]() 周長的最小值及此時點
周長的最小值及此時點![]() 的坐標;
的坐標;
(2)如圖2,在(1)問的條件下,點![]() 是直線
是直線![]() 上的一個動點,問:在
上的一個動點,問:在![]() 軸上是否存在
軸上是否存在![]() 點,使得
點,使得![]() 是以
是以![]() 為腰的等腰直角三角形?若存在,請直接寫出
為腰的等腰直角三角形?若存在,請直接寫出![]() 點及對應的
點及對應的![]() 點的坐標,若沒有,請說明理由.
點的坐標,若沒有,請說明理由.
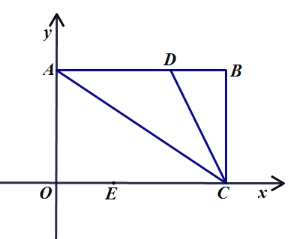
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com