
 如圖,四邊形ABCD中,∠C=40°,∠B=∠D=90°,E、F分別是BC、DC上的一點,當△AEF的周長最小時,∠EAF的度數(shù)為100°.
如圖,四邊形ABCD中,∠C=40°,∠B=∠D=90°,E、F分別是BC、DC上的一點,當△AEF的周長最小時,∠EAF的度數(shù)為100°. 分析 根據(jù)要使△AEF的周長最小,即利用點的對稱,使三角形的三邊在同一直線上,作出A關(guān)于BC和CD的對稱點A′,A″,即可得出∠AA′E+∠A″=∠HAA′=40°,進而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.
解答 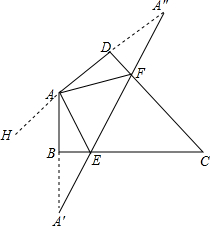 解:作A關(guān)于BC和CD的對稱點A′,A″,連接A′A″,交BC于E,交CD于F,
解:作A關(guān)于BC和CD的對稱點A′,A″,連接A′A″,交BC于E,交CD于F,
則A′A″即為△AEF的周長最小值.作DA延長線AH,
∵∠C=40°,
∴∠DAB=140°,
∴∠HAA′=40°,
∴∠AA′E+∠A″=∠HAA′=40°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=40°,
∴∠EAF=140°-40°=100°,
故答案為:100°.
點評 本題考查的是軸對稱-最短路線問題,涉及到平面內(nèi)最短路線問題求法以及三角形的外角的性質(zhì)和垂直平分線的性質(zhì)等知識,根據(jù)已知得出E,F(xiàn)的位置是解題關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖為某學(xué)校一塊空地,為了綠化環(huán)境,學(xué)校打算利用這塊空地種植花草,已知AB⊥BC,CD⊥BC,∠D=30°,AB=$\frac{1}{4}$CD=$\sqrt{6}$m,BC=3$\sqrt{2}$m,試求這塊空地的周長和面積.
如圖為某學(xué)校一塊空地,為了綠化環(huán)境,學(xué)校打算利用這塊空地種植花草,已知AB⊥BC,CD⊥BC,∠D=30°,AB=$\frac{1}{4}$CD=$\sqrt{6}$m,BC=3$\sqrt{2}$m,試求這塊空地的周長和面積.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2,-1 | B. | -2,1 | C. | -1,2 | D. | -2,-1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
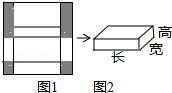 圖1是邊長為30cm的正方形紙板,裁掉陰影部分后將其折疊成如圖2所示的長方體盒子,已知該長方體的寬是高的2倍,這個長方體的高為5cm.
圖1是邊長為30cm的正方形紙板,裁掉陰影部分后將其折疊成如圖2所示的長方體盒子,已知該長方體的寬是高的2倍,這個長方體的高為5cm.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -1 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x=-5 | B. | x=2 | C. | x=4 | D. | x=5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 由①得y=$\frac{1}{2}$x,然后代入②消去y | B. | 由②得y=2x-5,然后代入①消去y | ||
| C. | 將①代入②消去x | D. | 由②得x=$\frac{1}{2}$(5+y),然后代入①消去x |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com