【題目】如圖拋物線y＝ax2+bx+c的對稱軸是x＝﹣1，與x軸的一個交點為（﹣5，0），則不等式ax2+bx+c＞0的解集為_____．
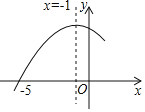
【答案】﹣5＜x＜3
【解析】
先根據拋物線的對稱性得到A點坐標（3，0），由y＝ax2+bx+c＞0得函數值為正數，即拋物線在x軸上方，然后找出對應的自變量的取值范圍即可得到不等式ax2+bx+c＞0的解集．
解：根據圖示知，拋物線y＝ax2+bx+c圖象的對稱軸是x＝﹣1，與x軸的一個交點坐標為（﹣5，0），
根據拋物線的對稱性知，拋物線y＝ax2+bx+c圖象與x軸的兩個交點關于直線x＝﹣1對稱，即
拋物線y＝ax2+bx+c圖象與x軸的另一個交點與（﹣5，0）關于直線x＝﹣1對稱，
∴另一個交點的坐標為（3，0），
∵不等式ax2+bx+c＞0，即y＝ax2+bx+c＞0，
∴拋物線y＝ax2+bx+c的圖形在x軸上方，
∴不等式ax2+bx+c＞0的解集是﹣5＜x＜3．
故答案為﹣5＜x＜3．
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y＝ax2+bx+c（a#0）的圖象的頂點在第一象限，且過點（0，1）和（﹣1，0）．下列結論：①ab＜0；②b2＞4ac；③0＜b＜1；④當x＜﹣1時，y＜0．其中正確結論的個數是（ ）
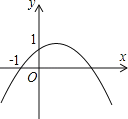
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商業集團新建一小車停車場，經測算，此停車場每天需固定支出的費用（設施維修費、車輛管理人員工資等）為800元．為制定合理的收費標準，該集團對一段時間每天小車停放輛次與每輛次小車的收費情況進行了調查，發現每輛次小車的停車費不超過5元時，每天來此處停放的小車可達1440輛次；若停車費超過5元，則每超過1元，每天來此處停放的小車就減少120輛次．為便于結算，規定每輛次小車的停車費x（元）只取整數，用y（元）表示此停車場的日凈收入，且要求日凈收入不低于2512元．（日凈收入＝每天共收取的停車費﹣每天的固定支出）
（1）當x≤5時，寫出y與x之間的關系式，并說明每輛小車的停車費最少不低于多少元；
（2）當x＞5時，寫出y與x之間的函數關系式（不必寫出x的取值范圍）；
（3）該集團要求此停車場既要吸引客戶，使每天小車停放的輛次較多，又要有較大的日凈收入．按此要求，每輛次小車的停車費應定為多少元？此時日凈收入是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了滿足師生的閱讀需求，某校圖書館藏書總量由2017年
萬冊增加到2019年
萬冊.
(1)求該校圖書館這兩年藏書總量的年均增長率;
(2)經統計知:在這兩年新增加的圖書中，中外古典名著所占的百分率恰好等于這兩年藏書總量的年均增長率，2019年中外古典名著冊數占藏書總量的
，而在2017年中外古典名著冊數僅占當年藏書總量的
，請求出
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地盛產櫻桃，一年一度的櫻桃節期間，很多果園推出了免費品嘗和優惠采摘活動，其中甲、乙兩家果園的櫻桃品質相同，銷售價格也相同，但推出了不同的采摘方案：
甲園 | 游客進園需購買 |
乙園 | 游客進園不需購買門票，采摘的櫻桃在一定數量以內按原價購買，超過部分打折購買 |
小明和爸爸、媽媽在櫻桃節期間也來采摘櫻桃，若設他們的櫻桃采摘量為
（千克）（出園時將自己采摘的櫻桃全部購買），在甲采摘園所需總費用為
（元）在乙采摘園所需總費用為
（元），圖中的折線
表示與之間的函數關系.
（1）①甲、乙兩果園的櫻桃單價為_____________元
千克；
②直接寫出的函數表達式：_________________，并在圖中補畫出的函數圖象；
（2）求出與之間的函數關系式；
（3）若小明一家當天所采摘的櫻桃不少于
千克，選擇哪個采摘園更劃算？請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了傳承優秀傳統文化，某校開展“經典誦讀”比賽活動，誦讀材料有《論語》，《三字經》，《弟子規》（分別用字母A，B，C依次表示這三個誦讀材料），將A，B，C這三個字母分別寫在3張完全相同的不透明卡片的正面上，把這3張卡片背面朝上洗勻后放在桌面上．小明和小亮參加誦讀比賽，比賽時小明先從中隨機抽取一張卡片，記錄下卡片上的內容，放回后洗勻，再由小亮從中隨機抽取一張卡片，選手按各自抽取的卡片上的內容進行誦讀比賽．
（1）小明誦讀《論語》的概率是 .
（2）請用列表法或畫樹狀圖法求小明和小亮誦讀兩個不同材料的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD內有一點P，PA＝5，PB＝
，PC＝
，將△BPC繞點B逆時針旋轉90°．
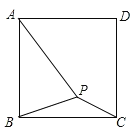
（1）畫出旋轉后的圖形；
（2）求點C和點P′的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線
經過點
和點
，與
軸交于點
.
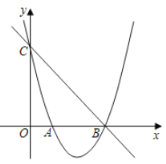
（1）求此拋物線的解析式；
（2）若點
是直線
下方的拋物線上一動點（不點
，重合），過點作軸的平行線交直線于點
，設點的橫坐標為
.
①用含的代數式表示線段
的長；
②連接
，
，求
的面積最大時點的坐標；
（3）設拋物線的對稱軸與交于點
，點
是拋物線的對稱軸上一點，
為軸上一點，是否存在這樣的點和點，使得以點、、、為頂點的四邊形是菱形？如果存在，請直接寫出點的坐標；如果不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】開學初，我縣某校開展“新學期、新征程，新氣象”入學系列教育活動，訓練兩天后，為了在合唱中給某班學生恰當地分配聲部，該校音樂教師李老師隨機抽取學生試唱，根據試唱情況把所抽學生分成A、B、C、D四種聲部等級，并根據等級統計結果繪制了如圖1和如圖2兩幅不完整的統計圖，請根據圖中提供的信息完成以下問題：
（1）扇形統計圖中D等對應的圓心角的度數是 °，補全條形統計圖；
（2）已知A等聲部的同學有一位是男生，李老師準備從這4位同學中隨機選擇兩位同學教其他同學，請用列表法或畫樹狀圖的方法求出選中的兩名同學恰好是一男一女的概率？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
