
已知二次函數y=ax2+bx的圖象經過點A(-5,0)和點B,其中點B在第一象限,且OA=OB,tan∠BAO=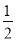
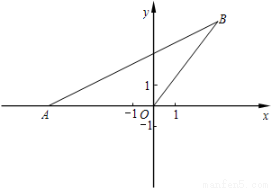
(1)求點B的坐標。
(2)求二次函數的解析式。
(3)過點B作直線BC平行于x軸,直線BC與二次函數圖象的另一個交點為C,連結AC,如果點P在x軸上,且△ABC和△PAB相似,求點P的坐標。
(1)點B的坐標是(3,4),(2)y=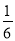 x2+
x2+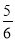 x;(3)點P的坐標為(6,0)或(
x;(3)點P的坐標為(6,0)或(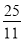 ,0).
,0).
【解析】
試題分析:(1)過點B作BD⊥x軸,垂足為點D,根據余切的定義可設BD=x,AD=2x,在Rt△ODB中根據勾股定理可計算出x,則BD=4,OD=3,所以點B的坐標是(3,4);
(2)利用待定系數法可確定二次函數的解析式;
(3)先確定C點的坐標為(-8,4),則BC=11,AB=4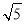 ,由CB∥x軸得到∠ABC=∠BAP,再分類討論:當△ABC∽△BAP;當△ABC∽△PAB,然后利用比例線段求AP的長,從而確定P點坐標.
,由CB∥x軸得到∠ABC=∠BAP,再分類討論:當△ABC∽△BAP;當△ABC∽△PAB,然后利用比例線段求AP的長,從而確定P點坐標.
試題解析:(1)過點B作BD⊥x軸,垂足為點D,如圖,
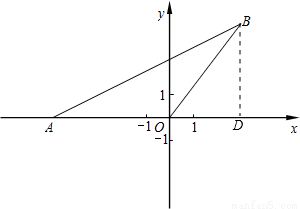
在Rt△ADB中,∠ADB=90°,tan∠BAO=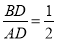
設BD=x,AD=2x,
∵OA=0B=5,
∴OD=2x-5,
在Rt△ODB中,∵OD2+BD2=OB2,
∴(2x-5)2+x2=52,
解得x1=4,x2=0(不合題意,舍去),
∴BD=4,OD=3,
∴點B的坐標是(3,4),
(2)根據題意得
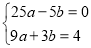 ,
,
解這個方程組,得
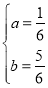 ,
,
∴二次函數的解析式是y=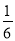 x2+
x2+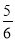 x;
x;
(3)∵直線BC平行于x軸,
∴C點的縱坐標為4,
設C點的坐標為(m,4).
由題意得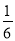 m2+
m2+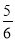 m=4,
m=4,
解得m1=3(不合題意,舍去),m2=-8,
∴C點的坐標為(-8,4),BC=11,AB=4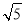
∵∠ABC=∠BAP,
①如果△ABC∽△BAP,那么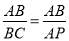
∴AP=11,點P的坐標為(6,0),
②如果△ABC∽△PAB,那么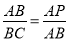 ,
,
∴AP=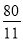 ,點P的坐標為(
,點P的坐標為(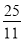 ,0),
,0),
綜上所述,點P的坐標為(6,0)或(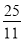 ,0).
,0).
考點:待定系數法求二次函數解析式.


科目:初中數學 來源:2014-2015學年黑龍江省哈爾濱市道里區九年級上學期期末調研測試數學試卷(解析版) 題型:填空題
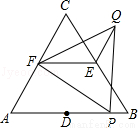
如圖,△ABC和△FPQ均是等邊三角形,點D、E、F分別是△ABC三邊的中點,點P在AB邊上,連接EF、QE.若AB=6,PB=1,則QE= 2 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣八年級上學期期中調研數學試卷(解析版) 題型:填空題
已知一直角三角形的木板,三邊的平方和為800 cm2,則斜邊長為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣八年級上學期期中調研數學試卷(解析版) 題型:選擇題
下列結論正確的是
A.有兩個銳角相等的兩個直角三角形全等
B.一條斜邊對應相等的兩個直角三角形全等
C.兩個等邊三角形全等
D.頂角和底邊對應相等的兩個等腰三角形全等
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市青春共同體九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,AB是⊙O的直徑,C是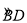 的中點,CE⊥AB于 E,BD交CE于點F.
的中點,CE⊥AB于 E,BD交CE于點F.
(1)求證:CF﹦BF;
(2)若CD=6,AC=8,求⊙O的半徑及CE的長。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市青春共同體九年級上學期期中考試數學試卷(解析版) 題型:填空題
△ABC中,∠A、∠B都是銳角,若sinA=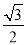 ,cosB=
,cosB=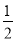 ,則∠C= .
,則∠C= .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省濰坊地區九年級上學期期末質量評估數學試卷(解析版) 題型:解答題
(本題滿分10分)市某樓盤準備以每平方米6 000元的均價對外銷售,由于國務院有關房地產的新政策出臺后,購房者持幣觀望,房地產開發商為了加快資金周轉,對價格經過兩次下調后,決定以每平方米4 860元的均價開盤銷售.
(1)求平均每次下調的百分率.
(2)某人準備以開盤價均價購買一套100平方米的住房,開發商給予以下兩種優惠方案以供選擇:①打9.8折銷售;②不打折,一次性送裝修費每平方米80元,試問哪種方案更優惠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com