Question

1．如圖，在平面直角坐標系中，點O為坐標原點，△ABC的頂點A在y軸的正半軸上，且OA=m，頂點B，C的坐標分別為（-m，0），（m，0），點D是線段AB上的一個動點（點D不與點A、B重合），點E是線段AC上的一點，且AE=BD，連接OD，DE，線段DE與線段OA相交于點F；
（1）求∠ODE的度數；
（2）當m=2+2$\sqrt{2}$，且△ODF為等腰三角形時，求點D的坐標；
（3）連接CD，過點C作CG⊥DE交線段DE的延長線于點G，過點F作FH∥AB交線段CG的延長線于點H，若∠ADE=∠CDE，求證：CH-2EG=$\frac{BD•DF}{AD}$．

Answer 1

分析 （1）只要證明△OBD≌△OAE，OD=OE，∠BOD=∠AOE，∠DOE=∠BOA=90°，推出△DOE是等腰直角三角形即可．
（2）分兩種情形討論即可解決問題①當點D是AB中點時，△DOF是等腰三角形，此時D（-1-$\sqrt{2}$，1+$\sqrt{2}$）．②當DF=DO時，∠DOF=∠DFO=∠ADO，推出AD=AO，求出BD即可解決問題．
（3）如圖3中，延長BA交CH的延長線于N，連接CF、OG．只要證明△FHG≌△CEG，推出EG=HG，由FA平分∠DAE，推出$\frac{AD}{AE}$=$\frac{DF}{EF}$，（角平分線性質定理），推出DF•AE=AD•EF，由BD=AE，推出DF•BD=AD•EF，推出$\frac{BD•DF}{AD}$=EF，CH-2EG=（GH+CG）-2EG=EF，延長即可證明．

解答 解：（1）如圖1中，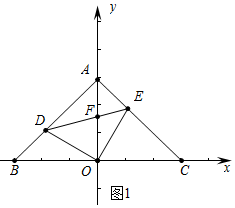

∵OA=OB=OC，OA⊥BC，
∴△ABC是等腰直角三角形，
∴∠OBD=∠OAE=45°，
在△OBD和△OAE中，
$\left\{\begin{array}{l}{OB=OA}\\{∠OBD=∠OAE}\\{BD=AE}\end{array}\right.$，
∴△OBD≌△OAE，
∴OD=OE，∠BOD=∠AOE，
∴∠DOE=∠BOA=90°，
∴∠ODE=45°．

（2）如圖2中，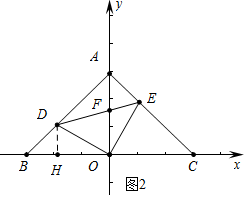

①當點D是AB中點時，△DOF是等腰三角形，此時D（-1-$\sqrt{2}$，1+$\sqrt{2}$）．
②當DF=DO時，∠DOF=∠DFO=∠ADO，
∴AD=AO，
∴BD=2$\sqrt{2}$+4-（2+2$\sqrt{2}$）=2，
∵∠DBH=∠BDH=45°，
∴DB=DH=$\sqrt{2}$，
∴D（-2-$\sqrt{2}$，$\sqrt{2}$），
綜上所述，滿足條件的點D坐標（-1-$\sqrt{2}$，1+$\sqrt{2}$）或（-2-$\sqrt{2}$，$\sqrt{2}$）．

（3）如圖3中，延長BA交CH的延長線于N，連接CF、OG．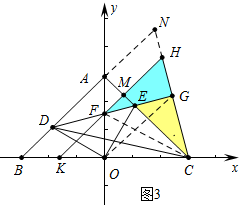

∵∠GDN=∠GDC，DG⊥CN，
∴∠N=∠DCG，
∴DN=DC，GN=GC，
∵CO=OB，
∴OG∥BN，∵KH∥BN，
∴OG∥BN，
∴∠GOC=45°，
∵∠FOC+∠FGC=180°，
∴F、O、C、G四點共圓，
∴∠GFC=∠GOC=45°，
∴∠GFC=∠GCF=45°，
∴FG=GC，
在△FHG和△CEG中，
$\left\{\begin{array}{l}{∠FGH=∠CGF}\\{∠HFG=∠ECG}\\{FG=GC}\end{array}\right.$，
∴△FHG≌△CEG，
∴EG=HG，
∵FA平分∠DAE，
∴$\frac{AD}{AE}$=$\frac{DF}{EF}$，（角平分線性質定理）
∴DF•AE=AD•EF，
∵BD=AE，
∴DF•BD=AD•EF，
∴$\frac{BD•DF}{AD}$=EF，CH-2EG=（GH+CG）-2EG=EF，
∴CH-2EG=$\frac{BD•DF}{AD}$．

點評 本題考查三角形綜合題、全等三角形的判定和性質、角平分線的性質定理、四點共圓等知識，解題的關鍵是學會利用四點共圓，角平分線的性質定理解決問題，題目比較難，知識點比較多，屬于中考壓軸題．