
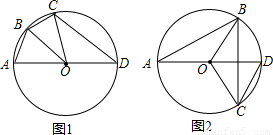
 ∠COA=∠BOA,從而可判斷CD∥BO;
∠COA=∠BOA,從而可判斷CD∥BO;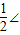 COA,
COA, ∠COA(圓周角定理),
∠COA(圓周角定理),

科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
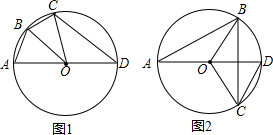 (1)如圖1,AD為⊙O的直徑,在圓上找一點B,將△AOB沿OB對折,和△COB能重合,連接CD,請問CD和BO有什么位置關系?并說明理由.
(1)如圖1,AD為⊙O的直徑,在圓上找一點B,將△AOB沿OB對折,和△COB能重合,連接CD,請問CD和BO有什么位置關系?并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com