

分析 (1)將C點坐標代入拋物線解析式可求k的值,由拋物線解析式求A,B兩點坐標;
(2)根據A、B、M、N四點坐標,將四邊形分割為兩個三角形和一個梯形求面積;
(3)只要使△DBC面積最大即可,由此求D點坐標;
解答 解:(1)將C(0,-3)代入拋物線y=x2-2x+k中,得k=-3,
∴拋物線解析式為y=x2-2x-3,
令y=0,得x=-1或3,
∴A(-1,0),B(3,0);
故答案為-3,(-1,0),(3,0);
(2)如圖(1),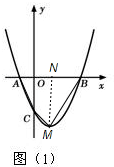
過M點作MN⊥AB,垂足為N,
由y=x2-2x-3=(x-1)2-4,可知M(1,-4),
∴S四邊形ABMC=S△ACO+S梯形OCMN+S△BMN=$\frac{1}{2}$×1×3+$\frac{1}{2}$×(3+4)×1+$\frac{1}{2}$×(3-1)×4=9;
(3)存在,如圖(2),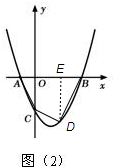
設D(m,m2-2m-3),
過D點作DE⊥AB,垂足為E,則
S四邊形ABDC=S△ACO+S梯形OCDE+S△BDE
=$\frac{1}{2}$×1×3+$\frac{1}{2}$×[3-(m2-2m-3)]×m+$\frac{1}{2}$×(3-m)×[-(m2-2m-3)]
=-$\frac{3}{2}$m2+$\frac{9}{2}$m+6,
∵-$\frac{3}{2}$<0,
∴當m=-$\frac{\frac{9}{2}}{-3}$=$\frac{3}{2}$時,S四邊形ABDC最大,此時D($\frac{3}{2}$,-$\frac{15}{4}$).
點評 本題考查了二次函數的綜合運用.關鍵是根據題意求拋物線解析式,將四邊形分割為三角形與梯形的面積和求解,同時考查了坐標系中,線段的垂直關系.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:初中數學 來源: 題型:填空題
 如圖,矩形ABCD中,把△ACD沿AC折疊到△ACD′,AD′與BC交于點E,若AD=8,DC=6,則BE的長為$\frac{7}{4}$.
如圖,矩形ABCD中,把△ACD沿AC折疊到△ACD′,AD′與BC交于點E,若AD=8,DC=6,則BE的長為$\frac{7}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | “奔跑吧,兄弟”節目的收視率 | B. | “神州十一號”飛船的零件合格率 | ||
| C. | 某種品牌節能燈的使用壽命 | D. | 全國植樹節中栽植樹苗的成活率 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 解不等式組:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x+1}{3}≥x-1}\end{array}\right.$,把解集表示在數軸上,并寫出所有非負整數解.
解不等式組:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x+1}{3}≥x-1}\end{array}\right.$,把解集表示在數軸上,并寫出所有非負整數解.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,過點A(2,0)的直線l與y軸交于點B,tan∠OAB=$\frac{1}{2}$,直線l上的點P位于y軸左側,且到y軸的距離為1.
如圖,在平面直角坐標系中,過點A(2,0)的直線l與y軸交于點B,tan∠OAB=$\frac{1}{2}$,直線l上的點P位于y軸左側,且到y軸的距離為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 銷售時段 | 銷售數量 | 銷售收入 | |
| A種型號 | B種型號 | ||
| 第一周 | 3臺 | 6臺 | 7650元 |
| 第二周 | 4臺 | 10臺 | 11800元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 甲、乙兩工程隊維修同一段路面,甲隊先清理路面,乙隊在甲隊清理后鋪設路面.乙隊在中途停工了一段時間,然后按停工前的工作效率繼續工作.在整個工作過程中,甲隊清理完的路面長y(米)與時間x(時)的函數圖象為線段OA,乙隊鋪設完的路面長y(米)與時間x(時)的函數圖象為折線BC-CD-DE,如圖所示,從甲隊開始工作時計時.
甲、乙兩工程隊維修同一段路面,甲隊先清理路面,乙隊在甲隊清理后鋪設路面.乙隊在中途停工了一段時間,然后按停工前的工作效率繼續工作.在整個工作過程中,甲隊清理完的路面長y(米)與時間x(時)的函數圖象為線段OA,乙隊鋪設完的路面長y(米)與時間x(時)的函數圖象為折線BC-CD-DE,如圖所示,從甲隊開始工作時計時.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com