
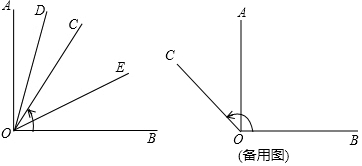
分析 (1)根據角平分線的定義,OD、OE分別平分∠AOC和∠BOC,則可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)①結合角的特點,∠DOE=∠DOC+∠COE,求得結果進行判斷和計算;②分三種情況討論:當90°<n≤180°時,當180°<n≤270°時,當270°<n<360°,分別求得∠DOE的度數;
(3)根據(2)中方法進行分類討論,即可得出∠DOE的度數.
解答 解:(1)∵OD、OE分別平分∠AOC和∠BOC,
∴∠COE=$\frac{1}{2}$∠COB=30°,∠COD=$\frac{1}{2}$∠AOC=15°,
∴∠DOE=∠COE+∠COD=45°;
故答案為:45°;
(2)①∠DOE的大小不變,等于45°,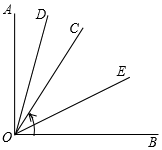
理由:∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC+∠COE
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠AOC+∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
②分三種情況: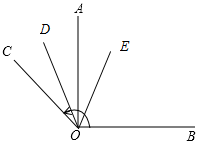
當90°<n≤180°時,∠DOE的大小不變,等于45°,
理由:如圖所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE-∠DOC
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°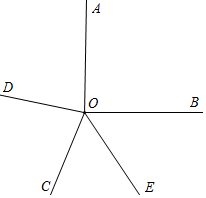
=45°;
當180°<n≤270°時,∠DOE的大小不變,等于135°,
理由:如圖所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE+∠DOC
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC+∠AOC)
=$\frac{1}{2}$(360°-∠AOB)
=$\frac{1}{2}$×270°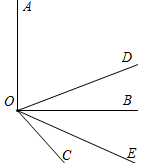
=135°;
當270°<n<360°時,∠DOE的大小不變,等于45°,
理由:如圖所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC-∠COE
=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC
=$\frac{1}{2}$(∠AOC-∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
(3)在射線OC旋轉過程中,∠DOE的度數為$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
理由:當0<n≤180°時,∠DOE=$\frac{1}{2}$a;
當180°<n≤180°+a時,∠DOE=180°-$\frac{1}{2}$a;
當180°+a<n<360°時,∠DOE=$\frac{1}{2}$a;
綜上所述,∠DOE的度數為$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
點評 本題主要考查了角的和差關系的運用以及角平分線的定義的運用,即從一個角的頂點出發,把這個角分成相等的兩個角的射線叫做這個角的平分線.解決問題的關鍵是畫出圖形進行分類討論,分類時注意不能遺漏,也不能重復.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0.358×105 | B. | 3.58×104 | C. | 35.8×103 | D. | 358×102 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知△ABC≌△DEF,點B與點E是對應點,點A與點D是對應點,下列說法不一定成立的是( )
如圖,已知△ABC≌△DEF,點B與點E是對應點,點A與點D是對應點,下列說法不一定成立的是( )| A. | AB=DE | B. | AC=DF | C. | BE=EC | D. | BE=CF |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
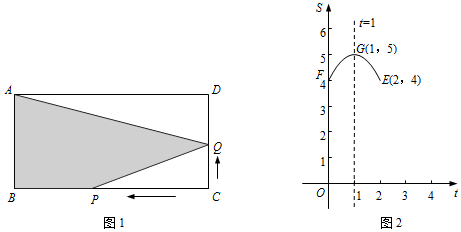
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com